题目内容
 如图,用3个边长为1的正方形组成一个对称图形,则能将其完整盖住的圆的最小半径为
如图,用3个边长为1的正方形组成一个对称图形,则能将其完整盖住的圆的最小半径为5
| ||
| 16 |
5
| ||
| 16 |
分析:设“品”字下边两端点为AB,中点为E;上边两端点为CD,中点为F,圆心O必在对称轴EF上,OA=OB=OC=OD=R,AE=EB=1,CF=FD=0.5,EF=2
又设OE=x,则OF=2-x,由勾股定理得出方程12+x2=R2,0.52+(2-x)2=R2,求出方程组的解即可.
又设OE=x,则OF=2-x,由勾股定理得出方程12+x2=R2,0.52+(2-x)2=R2,求出方程组的解即可.
解答:解:设“品”字下边两个端点为A、B,线段AB中点为E,上边两端点为CD,中点为F,圆心O必在对称轴EF上,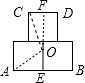
OA=OB=OC=OD=R,AE=EB=1,CF=FD=0.5,EF=2
又设OE=x,则OF=2-x
由勾股定理得:AE2+OE2=OA2,CF2+OF2=OC2,
12+x2=R2,0.52+(2-x)2=R2,
x=
,r=
,
即能盖住“品”字的最小圆纸片半径为
,
故答案为:
.

OA=OB=OC=OD=R,AE=EB=1,CF=FD=0.5,EF=2
又设OE=x,则OF=2-x
由勾股定理得:AE2+OE2=OA2,CF2+OF2=OC2,
12+x2=R2,0.52+(2-x)2=R2,
x=
| 13 |
| 16 |
5
| ||
| 16 |
即能盖住“品”字的最小圆纸片半径为
5
| ||
| 16 |
故答案为:
5
| ||
| 16 |
点评:本题考查了圆的性质,勾股定理,方程的应用,解此题的关键是得出关于R、x的方程.

练习册系列答案
相关题目
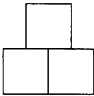 如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为( )
如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.
如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径. 如图,用三个边长为a的等边三角形拼成如图(1)所示的等腰梯形,现将这个等腰梯形截成四个全等的等腰梯形(图中的1,2,3,4部分).然后将其中的一个等腰梯形按照上述方法再截成四个全等的等腰梯形.如此重复下去….求第n次截得的一个等腰梯形的周长和面积.
如图,用三个边长为a的等边三角形拼成如图(1)所示的等腰梯形,现将这个等腰梯形截成四个全等的等腰梯形(图中的1,2,3,4部分).然后将其中的一个等腰梯形按照上述方法再截成四个全等的等腰梯形.如此重复下去….求第n次截得的一个等腰梯形的周长和面积.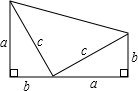 如图:用两个边长为a,b,c的直角三角形拼成一个直角梯形,试用不同的方法计算这个图形的面积,你能发现什么结论?
如图:用两个边长为a,b,c的直角三角形拼成一个直角梯形,试用不同的方法计算这个图形的面积,你能发现什么结论?