题目内容
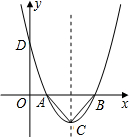 一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点(m为常数),记抛物线顶点为C,且AC⊥BC.
一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点(m为常数),记抛物线顶点为C,且AC⊥BC.(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若m小于0,那么(2)中的抛物线经过怎么样的平移可以使顶点在坐标原点?
分析:(1)设对称轴与x轴的交点为E,根据点A、B的坐标求出AB的长度以及对称轴解析式,然后根据等腰直角三角形的性质求出CE的长度,从而得解;
(2)根据顶点坐标设出抛物线的顶点式解析式,然后把点A的坐标代入解析式求解即可;
(3)根据m<0判断出顶点所在的象限,然后根据点的平移变换解答.
(2)根据顶点坐标设出抛物线的顶点式解析式,然后把点A的坐标代入解析式求解即可;
(3)根据m<0判断出顶点所在的象限,然后根据点的平移变换解答.
解答: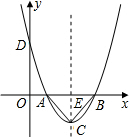 解:(1)如图,∵A(m-2,0),B(m+2,0),
解:(1)如图,∵A(m-2,0),B(m+2,0),
∴AB=(m+2)-(m-2)=m+2-m+2=4,
∵
=m,
∴抛物线对称轴为x=m,
∵抛物线顶点为C,且AC⊥BC,
∴△ABC是等腰直角三角形,且CE=
AB=
×4=2,
∴点C的坐标为(m,-2);
(2)设抛物线解析式为y=a(x-m)2-2,
则a(m-2-m)2-2=0,
解得a=
,
∴抛物线解析式为y=
(x-m)2-2;
(3)∵m<0,
∴顶点坐标(m,-2)在第三象限,
∴抛物线y=
(x-m)2-2向右平移(-m)个单位,向上平移2个单位可以使顶点在坐标原点.
 解:(1)如图,∵A(m-2,0),B(m+2,0),
解:(1)如图,∵A(m-2,0),B(m+2,0),∴AB=(m+2)-(m-2)=m+2-m+2=4,
∵
| m+2+m-2 |
| 2 |
∴抛物线对称轴为x=m,
∵抛物线顶点为C,且AC⊥BC,
∴△ABC是等腰直角三角形,且CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴点C的坐标为(m,-2);
(2)设抛物线解析式为y=a(x-m)2-2,
则a(m-2-m)2-2=0,
解得a=
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
(3)∵m<0,
∴顶点坐标(m,-2)在第三象限,
∴抛物线y=
| 1 |
| 2 |
点评:本题是对二次函数的综合考查,点的坐标,两点间的距离,待定系数法求二次函数解析式,抛物线的顶点式解析式的利用,以及平移变换的性质,难度不大,熟悉用字母表示数是解题的关键.

练习册系列答案
相关题目
 一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.
一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC. 一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.
一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.