题目内容
【题目】在平面直角坐标系中xOy中,抛物线![]() 的顶点在x轴上.
的顶点在x轴上.
(1)求抛物线的表达式;
(2)点Q是x轴上一点,
①若在抛物线上存在点P,使得∠POQ=45°,求点P的坐标;
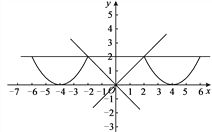
②抛物线与直线y=2交于点E,F(点E在点F的左侧),将此抛物线在点E,F(包含点E和点F)之间的部分沿x轴平移n个单位后得到的图象记为G,若在图象G上存在点P,使得∠POQ=45°,求n的取值范围.
【答案】(1)抛物线的表达式为![]() ;
;
(2)①点P的坐标为![]() 或
或 ![]() ②n的取值范围是
②n的取值范围是![]()
【解析】试题分析:(1)把函数解析式化为顶点式, ![]() , 因顶点在x轴上,可得m-2=0,即m=2,即可求得函数的解析式
, 因顶点在x轴上,可得m-2=0,即m=2,即可求得函数的解析式![]() ;(2)由∠POQ=45°可知点P是直线y=x与抛物线的交点,令
;(2)由∠POQ=45°可知点P是直线y=x与抛物线的交点,令![]() ,解得x的值即可得点P的坐标;(3)当E点移动到点(2,2)时,n=2,当F点移动到点(-2,2)时,n=-6,由图象可知,符合题意的n的取值范围是
,解得x的值即可得点P的坐标;(3)当E点移动到点(2,2)时,n=2,当F点移动到点(-2,2)时,n=-6,由图象可知,符合题意的n的取值范围是![]() .
.
试题解析:
(1)![]() .
.
由题意,可得m-2=0.
∴![]() .
.
∴![]() .
.
(2)①由题意得,点P是直线![]() 与抛物线的交点.
与抛物线的交点.
∴![]() .
.
解得 ![]() ,
, ![]() .
.
∴P点坐标为![]() 或
或 ![]() .
.
②当E点移动到点(2,2)时,n=2.
当F点移动到点(-2,2)时,n=-6.
由图象可知,符合题意的n的取值范围是![]() .
.

练习册系列答案
相关题目