题目内容
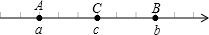如图，已知数轴上点A、B、C所对应的数a、b、c都不为0，且C是AB的中点．如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0，那么原点O的位置在
- A.线段AC上
- B.线段CA的延长线上
- C.线段BC上
- D.线段CB的延长线上
A
分析：数轴与绝对值结合，先根据绝对值的性质，判断出a，b，c的大致取值，再根据图形和已知等式确定原点位子．
解答：C是AB的中点，则a+b=2c，
因而 ①，a+b-2c=0?|a+b-2c|=0，
②，a-2c=-b?|a-2c|=|-b|=|b|，
③，b-2c=-a?|b-2c|=|-a|=|a|，
所以，原式=|a+b|-|b|+|a|-0=0?|a+b|=|b|-|a|，
因为|a+b|＞0?a，b异号，并且|b|＞|a|，
就是|OB|＞|OA|，因而点O在A，C之间．
故选A．
点评：本题考查了数轴与绝对值结合．
分析：数轴与绝对值结合，先根据绝对值的性质，判断出a，b，c的大致取值，再根据图形和已知等式确定原点位子．
解答：C是AB的中点，则a+b=2c，
因而 ①，a+b-2c=0?|a+b-2c|=0，
②，a-2c=-b?|a-2c|=|-b|=|b|，
③，b-2c=-a?|b-2c|=|-a|=|a|，
所以，原式=|a+b|-|b|+|a|-0=0?|a+b|=|b|-|a|，
因为|a+b|＞0?a，b异号，并且|b|＞|a|，
就是|OB|＞|OA|，因而点O在A，C之间．
故选A．
点评：本题考查了数轴与绝对值结合．
练习册系列答案
相关题目
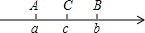如图，已知数轴上点A、B、C所对应的数a、b、c都不为0，且C为AB之中点，如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0，则原点O的位置是（ ）