题目内容
已知等腰△ABC的周长为36cm,底边BC上的高12cm,则cosB的值为 ( )
A.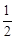 | B.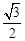 | C.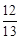 | D.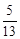 |
D
分析:设AB=xcm,则AC=AB=xcm,BC=(36-2x)cm,求出BD=DC=1/2BC=(18-x)cm,在Rt△ADB中,由勾股定理得出方程x2=122+(18-x)2,求出x=13,求出AB=13cm,BD=5cm即可。
解答:
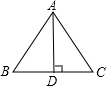
设AB=xcm,则AC=AB=xcm,BC=(36-2x)cm,
∵AB=AC,AD是高,
∴BD=DC=1/2BC=(18-x)cm,
在Rt△ADB中,由勾股定理得:AB2=AD2+BD2,
x2=122+(18-x)2,
∴x=13,
即AB=13cm,BD=5cm,
∴cosB=BD/AB=5/13。
故选D。

练习册系列答案
相关题目
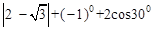
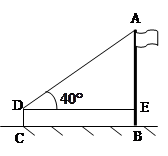
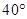 ,已知测角仪器的高CD=1.5米,求旗杆AB的高.(精确到0.1米)(供选用的数据:
,已知测角仪器的高CD=1.5米,求旗杆AB的高.(精确到0.1米)(供选用的数据: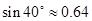 ,
,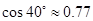 ,
,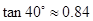 )
)
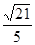
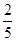


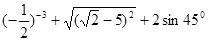
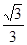 ,则cosB=_______;
,则cosB=_______;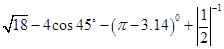 .
.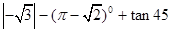 º
º 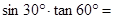 .
.