题目内容
【题目】如图,在![]() 中,AC=BC,∠ACB=90o,D为AB的中点,E为线段AD上一点,过E点的线段FG交CD的延长线于点G,交AC于点F,且
中,AC=BC,∠ACB=90o,D为AB的中点,E为线段AD上一点,过E点的线段FG交CD的延长线于点G,交AC于点F,且![]() ,分别延长
,分别延长![]() 、
、![]() 交于点H,若EH平分∠AEG,HD平分∠CHG。则下列说法:①∠GDH=45o;②GD=ED; ③EF=2DM; ④CG=2DE+AE,正确的是_________________ (填番号)
交于点H,若EH平分∠AEG,HD平分∠CHG。则下列说法:①∠GDH=45o;②GD=ED; ③EF=2DM; ④CG=2DE+AE,正确的是_________________ (填番号)

【答案】①②④
【解析】
①作DQ⊥CH,DN⊥BH,先证明Rt△CQD≌Rt△BND,得出∠QCD=∠NBD;再证明Rt△CHD≌Rt△BHD,得出∠HDC=∠HDB,即∠HDE=∠HDG;最后根据∠ADG=90°,即可得出
②EH平分∠AEG,得出∠AEH=∠GEH,从而得出补角相等,即∠AEC=∠GEC,进而证明△AEC≌△GEC,得出∠A=∠FGC=45°,根据内角和得出∠GED=∠FGC=45°即可得出
③由∠A=∠DGE证明△AEF≌△GED,得出EF=DE=DG;根据已知求出∠HDA =∠DEG=45°
得出EM=DM,即△EDM为直角三角形,再根据勾股定理即可求出DE与DM的关系,从而得出EF与DM的关系
④根据已知,得出AD=CD;由DE=GD,AD=AE+DE ,代入CG=CD+DG,即可得出

∵∠ACB=90°,AC=BC,
∴∠A=∠CBA=45°
∵D为AB的中点,AC=BC,
∴CD⊥AB
∴∠DCB=∠CBA=45°
∴CD=BD
作DQ⊥CH,DN⊥BH
∴∠CQD=∠DNB=90°
∵HD平分∠CHG
∴DQ=DN
∴在Rt△CQD和Rt△BND中,
![]()
∴Rt△CQD≌Rt△BND
∴∠QCD=∠NBD
∵HD平分∠CHG
∴∠EHD=∠DHG
∴在Rt△CHD和Rt△BHD中,
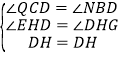
∴Rt△CHD≌Rt△BHD(AAS)
∴∠HDC=∠HDB
∵CD⊥AB
∴∠ADC=∠CDB=∠ADG=∠BDG=90o
∴∠HDC-∠ADC=∠HDB-∠BDG
∴∠HDE=∠HDG
∵∠ADG=90°
∴∠HDE=∠HDG=45°
∴∠GDH=45°
故①正确
②∵EH平分∠AEG,
∴∠AEH=∠GEH
∴∠AEC=∠GEC
∴在△AEC和△GEC中,

∴△AEC≌△GEC(SAS)
∴∠A=∠FGC
∵∠ACB=90°,AC=BC
∴∠A=∠CBA=45°
∴∠FGC=45°
∴AC=BC,O为AB中点, CD⊥AB
∴∠ADG=90°
∴∠GED=∠FGC=45°
∴GD=ED
故②正确
③∵∠ACB=90°,AC=BC,D为AB的中点
∴∠CAB=∠CBA=45°,CD⊥AB
∴∠ADG=90°,
由②得DE=GD
∴∠DEG=∠DGE=45°
∴∠A=∠DGE=45°
∴在△AEF和△GED中,

∴△AEF≌△GED(ASA)
∴EF=DE=DG
∵∠GDH=45°
∴∠HDA=45°
∴∠HDA =∠DEG=45°
∴EM=DM
∴∠EMD =90°,
∴在Rt△EMD中,∠EMD =90°
∴DE=![]() =
=![]()
∴EF=DE=![]()
∴③EF=2DM错误
④∵∠ACB=90°,AC=BC,
∴∠A=∠CBA=45°
∵D为AB的中点,AC=BC,
∴CD⊥AB
∴∠A=∠ACD=45°
∴AD=CD
∵CG=CD+DG
∴CG=AD+DG
由②得DE=GD
∴CG=AD+DE
∵AD=AE+DE
∴CG=AE+DE+DE
∴CG=AE+2DE
故④正确
综上,故答案为:①②④

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案






