题目内容
如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.

(1)问运动多少时BC=8(单位长度)?
(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式
=3,若存在,求线段PD的长;若不存在,请说明理由.

(1)问运动多少时BC=8(单位长度)?
(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是
4或40
4或40
;(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式
| BD-AP | PC |
分析:(1)设运动t秒时,BC=8(单位长度),然后分点B在点C的左边和右边两种情况,根据题意列出方程求解即可;
(2)由(1)中求出的运动时间即可求出点B在数轴上表示的数;
(3)随着点B的运动,分别讨论当点B和点C重合、点C在点A和B之间及点A与点C重合时的情况.
(2)由(1)中求出的运动时间即可求出点B在数轴上表示的数;
(3)随着点B的运动,分别讨论当点B和点C重合、点C在点A和B之间及点A与点C重合时的情况.
解答:解:(1)设运动t秒时,BC=8单位长度,
①当点B在点C的左边时,
由题意得:6t+8+2t=24
解得:t=2(秒);
②当点B在点C的右边时,
由题意得:6t-8-2t=24
解得:t=8(秒).
(2)当运动2秒时,点B在数轴上表示的数是4;
当运动8秒时,点B在数轴上表示的数是40.
(3)存在关系式
=3.
设运动时间为t秒,
1)当t=3时,点B和点C重合,点P在线段AB上,0<PC≤2,且BD=CD-4,AP+3PC=AB+2PC=2+2PC,
当PC=1时,BD=AP+3PC,即
=3;
2)当3<t<
时,点C在点A和点B之间,0<PC<2,
①点P在线段AC上时,BD=CD-BC=4-BC,AP+3PC=AC+2PC=AB-BC+2PC=2-BC+2PC,
当PC=1时,有BD=AP+3PC,即
=3;
点P在线段BC上时,BD=CD-BC=4-BC,AP+3PC=AC+4PC=AB-BC+4PC=2-BC+4PC,
当PC=
时,有BD=AP+3PC,即
=3;
3°当t=
时,点A与点C重合,0<PC≤2,BD=CD-AB=2,AP+3PC=4PC,
当PC=
时,有BD=AP+3PC,即
=3;
4°当
<t<
时,0<PC<4,BD=CD-BC=4-BC,AP+3PC=AB-BC+4PC=2-BC+4PC,
PC=
时,有BD=AP+3PC,即
=3.
①当点B在点C的左边时,
由题意得:6t+8+2t=24
解得:t=2(秒);
②当点B在点C的右边时,
由题意得:6t-8-2t=24
解得:t=8(秒).
(2)当运动2秒时,点B在数轴上表示的数是4;
当运动8秒时,点B在数轴上表示的数是40.
(3)存在关系式
| BD-AP |
| PC |
设运动时间为t秒,
1)当t=3时,点B和点C重合,点P在线段AB上,0<PC≤2,且BD=CD-4,AP+3PC=AB+2PC=2+2PC,
当PC=1时,BD=AP+3PC,即
| BD-AP |
| PC |
2)当3<t<
| 13 |
| 4 |
①点P在线段AC上时,BD=CD-BC=4-BC,AP+3PC=AC+2PC=AB-BC+2PC=2-BC+2PC,
当PC=1时,有BD=AP+3PC,即
| BD-AP |
| PC |
点P在线段BC上时,BD=CD-BC=4-BC,AP+3PC=AC+4PC=AB-BC+4PC=2-BC+4PC,
当PC=
| 1 |
| 2 |
| BD-AP |
| PC |
3°当t=
| 13 |
| 4 |
当PC=
| 1 |
| 2 |
| BD-AP |
| PC |
4°当
| 13 |
| 4 |
| 7 |
| 2 |
PC=
| 1 |
| 2 |
| BD-AP |
| PC |
点评:本题考查两点间的距离,并综合了数轴、一元一次方程和线段长短的比较,难度较大,注意对第三问进行分情况讨论,不要漏解.

练习册系列答案
相关题目

 (1)解不等式组:
(1)解不等式组: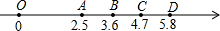 (2013•白下区二模)如图在数轴上有O、A、B、C、D五点,根据图中各点所表示的数,判断
(2013•白下区二模)如图在数轴上有O、A、B、C、D五点,根据图中各点所表示的数,判断
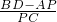 =3,若存在,求线段PD的长;若不存在,请说明理由.
=3,若存在,求线段PD的长;若不存在,请说明理由.