题目内容
 (1)解不等式组:
(1)解不等式组:
|
(2)如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
①求证:△ACD≌△BCE;
②若∠D=50°,求∠B的度数.
分析:(1)根据不等式的性质即可推出x的解集,画出数轴表示出x的解集即可;
(2)①根据已知可推出AC=BC,∠1=∠2=∠3,即可推出△ACD≌△BCE;②根据△ACD≌△BCE,推出∠A=∠B,∠D=∠E=50°,因此∠A+∠B=360°-(∠1+∠2+∠3)-(∠D+∠E)=80°,即可推出∠B的度数.
(2)①根据已知可推出AC=BC,∠1=∠2=∠3,即可推出△ACD≌△BCE;②根据△ACD≌△BCE,推出∠A=∠B,∠D=∠E=50°,因此∠A+∠B=360°-(∠1+∠2+∠3)-(∠D+∠E)=80°,即可推出∠B的度数.
解答:(1)解:∵解不等式组:
,
∴解①得:x>2,
解②得:x≤3,
∴2<x≤3;
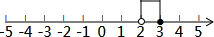
(2)①证明:∵C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,
∴AC=BC,∠1=∠2=∠3,
∵CD=CE,
∴△ACD≌△BCE,
②解:∵△ACD≌△BCE,∠D=50°,
∴∠A=∠B,∠D=∠E=50°,
∵∠1+∠2+∠3=180°,
∴∠A+∠B=360°-(∠1+∠2+∠3)-(∠D+∠E)=80°,
∴∠B=40°.
|
∴解①得:x>2,
解②得:x≤3,
∴2<x≤3;
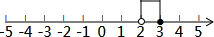
(2)①证明:∵C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,
∴AC=BC,∠1=∠2=∠3,
∵CD=CE,
∴△ACD≌△BCE,
②解:∵△ACD≌△BCE,∠D=50°,
∴∠A=∠B,∠D=∠E=50°,
∵∠1+∠2+∠3=180°,
∴∠A+∠B=360°-(∠1+∠2+∠3)-(∠D+∠E)=80°,
∴∠B=40°.
点评:本题主要考查解一元一次不等式组、全等三角形的判定和性质、在数轴上表示不等式的解集,关键在于正确的解不等式组求得解集,证明△ACD≌△BCE.

练习册系列答案
相关题目
 (1)计算:4cos45°+(π+3)0-
(1)计算:4cos45°+(π+3)0-