题目内容
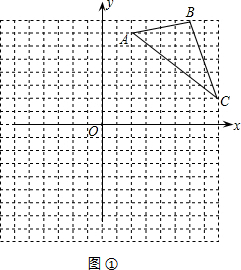 如图1,△ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),
如图1,△ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),(1)以O点为位似中心,在第三象限内作出△A1B1C1,使△A1B1C1与△ABC的位似比为1:2;画出图形.
(2)分别写出A1,B1,C1的坐标.
(3)如果△ABC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
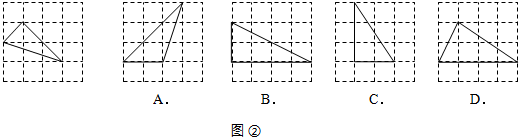
(4)如图2,下列四个三角形,与图2中的三角形相似的是
B
B
.
分析:(1)连接AO并延长至A1,使A1O=
AO,连接BO并延长至B1,使B1O=
BO,连接CO并延长至C1,使C1O=
CO,然后顺次连接即可得解;
(2)根据平面直角坐标系写出即可;
(3)根据变换后的点的坐标的横坐标与纵坐标都是变换前的坐标的相反数的一半,写出即可;
(4)先根据勾股定理求出三角形的三边的长,并求出比值,然后利用勾股定理求出四个选项中的三角形的三边的比,再根据三边对应成比例,两三角形相似判断即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据平面直角坐标系写出即可;
(3)根据变换后的点的坐标的横坐标与纵坐标都是变换前的坐标的相反数的一半,写出即可;
(4)先根据勾股定理求出三角形的三边的长,并求出比值,然后利用勾股定理求出四个选项中的三角形的三边的比,再根据三边对应成比例,两三角形相似判断即可.
解答: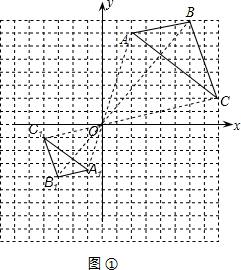 解:(1)如图所示,△A1B1C1即为所求作的三角形;
解:(1)如图所示,△A1B1C1即为所求作的三角形;
(2)点A1,B1,C1的坐标分别为A1(-1,-3.5),B1(-3,-4),C1(-4,-1);
(3)点M′的坐标为(-
x,-
y);
(4)根据勾股定理,三角形的三边分别为:
=
,
=2
,
=
,
所以三边之比为
:2
:
=1:2:
,
A、三角形三边之比为2:
:3
=
:
:3;
B、三角形三边之比为2:4:
=1:2:
;
C、三角形三边之比为2:3:
;
D、三角形三边之比为
:
:4,
根据三边对应成比例,两三角形相似可得与图2中的三角形相似的是B.
故答案为:B.
 解:(1)如图所示,△A1B1C1即为所求作的三角形;
解:(1)如图所示,△A1B1C1即为所求作的三角形;(2)点A1,B1,C1的坐标分别为A1(-1,-3.5),B1(-3,-4),C1(-4,-1);
(3)点M′的坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
(4)根据勾股定理,三角形的三边分别为:
| 12+12 |
| 2 |
| 22+22 |
| 2 |
| 12+32 |
| 10 |
所以三边之比为
| 2 |
| 2 |
| 10 |
| 5 |
A、三角形三边之比为2:
| 10 |
| 2 |
| 2 |
| 5 |
B、三角形三边之比为2:4:
| 20 |
| 5 |
C、三角形三边之比为2:3:
| 13 |
D、三角形三边之比为
| 5 |
| 13 |
根据三边对应成比例,两三角形相似可得与图2中的三角形相似的是B.
故答案为:B.
点评:本题考查了利用位似变换作图,坐标与图形的变化,勾股定理的应用,相似三角形的判定,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
 21、如图,三角形ABC三个顶点分别是A(2,2),B(3,4),C(5,3).将三角形向下平移3个单位长度,各个顶点的坐标变为多少?画出平移后的图形.
21、如图,三角形ABC三个顶点分别是A(2,2),B(3,4),C(5,3).将三角形向下平移3个单位长度,各个顶点的坐标变为多少?画出平移后的图形. (2012•石家庄二模)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )
(2012•石家庄二模)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )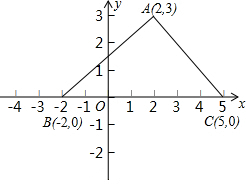 如图,三角形ABC三个顶点的坐标分别为A(2,3),B(-2,0),C(5,O),将三角形ABC沿x轴负方向平移2个单位,再沿y轴负方向平移1个单位,得到三角形A1B1C1.
如图,三角形ABC三个顶点的坐标分别为A(2,3),B(-2,0),C(5,O),将三角形ABC沿x轴负方向平移2个单位,再沿y轴负方向平移1个单位,得到三角形A1B1C1. 如图,三角形ABC三个项点坐标分别为A(3,-2),B(0,2),C(0,-5),将三角形ABC沿y轴正方向平移2个单位,再沿x轴负方向平移l个单位,得到三角形A1B1C1.
如图,三角形ABC三个项点坐标分别为A(3,-2),B(0,2),C(0,-5),将三角形ABC沿y轴正方向平移2个单位,再沿x轴负方向平移l个单位,得到三角形A1B1C1.