题目内容
在一个三角形中,如果一个角是另一个角的2倍,我们称这种三角形为倍角三角形.如图1,倍角△ABC中,∠A=2∠B,∠A、∠B、∠C的对边分别记为a,b,c,倍角三角形的三边a,b,c有什么关系呢?让我们一起来探索.
(1)我们先从特殊的倍角三角形入手研究.请你结合图形填空:
| 三三角形角形 | 角的已知量 |
|
| ||||
| 图2 | ∠A=2∠B=90° | ||||||
| 图3 | ∠A=2∠B=60° |
(3)请你运用(2)中的结论解决下列问题:若一个倍角三角形的两边长为5,6,求第三边长. (直接写出结论即可)
分析:(1)图2的三角形,显然是等腰直角三角形,可设斜边c为2,那么a=b=
,即可求得
、
的值,图3的解法同上.
(2)由(1)的结论,可猜测a、b、c的等量关系应该是
=
,可通过构造相似三角形来证明;延长CA至D,是得AD=AB;那么∠CAB=2∠A=2∠CBA,再加上公共角∠C,即可证得△CBD∽△CAB,由此得到所求的结论.
(3)将已知的边长代入(2)的结论进行计算即可.
| 2 |
| a |
| b |
| b+c |
| a |
(2)由(1)的结论,可猜测a、b、c的等量关系应该是
| a |
| b |
| b+c |
| a |
(3)将已知的边长代入(2)的结论进行计算即可.
解答:解:(1)
;(2分)
(2)猜测a,b,c的关系是
=
延长CA至D,使AD=AB(如图4);
∵AD=AB,∴∠D=∠ABD,
∴∠CAB=∠D+∠ABD=2∠D,
∵∠CAB=2∠CBA,
∴∠D=∠CBA,
又∵∠C=∠C,
∴△CBD∽△CAB,
∴
=
即
=
.(4分)
(3)①当a=5,b=6时,
由(2)得:
=
,解得c=-
(不合题意舍去);
②当a=6,b=5时,
=
,解得c=
;
③当a=5,c=6时,
=
,解得b=
-3(负值舍去);
④当a=6,c=5时,
=
,解得b=4(负值舍去);
⑤当b=5,c=6时,
=
,解得a=
(负值舍去);
⑥当b=6,c=5时,
=
,解得a=
(负值舍去).
综上可知:第三边的长为
或
或
-3或4或
.
| 三角形 | 角的已知量 |
|
| ||||
| 图2 | ∠A=2∠B=90° |
|
| ||||
| 图3 | ∠A=2∠B=60° |
|
|
(2)猜测a,b,c的关系是
| a |
| b |
| b+c |
| a |
∵AD=AB,∴∠D=∠ABD,
∴∠CAB=∠D+∠ABD=2∠D,
∵∠CAB=2∠CBA,
∴∠D=∠CBA,
又∵∠C=∠C,
∴△CBD∽△CAB,
∴
| CB |
| CA |
| CD |
| CB |
| a |
| b |
| b+c |
| a |
(3)①当a=5,b=6时,
由(2)得:
| 5 |
| 6 |
| 6+c |
| 5 |
| 11 |
| 6 |
②当a=6,b=5时,
| 6 |
| 5 |
| 5+c |
| 6 |
| 11 |
| 5 |
③当a=5,c=6时,
| 5 |
| b |
| b+6 |
| 5 |
| 34 |
④当a=6,c=5时,
| 6 |
| b |
| b+5 |
| 6 |
⑤当b=5,c=6时,
| a |
| 5 |
| 5+6 |
| a |
| 55 |
⑥当b=6,c=5时,
| a |
| 6 |
| 6+5 |
| a |
| 66 |
综上可知:第三边的长为
| 55 |
| 66 |
| 34 |
| 11 |
| 5 |
点评:此题主要考查的是相似三角形的判定和性质,要注意的是(3)题的情况较多,一定要分类讨论,不要漏解.

练习册系列答案
相关题目
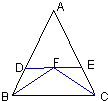 25、阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,请你用“等角对等边”的知识说明DE=BD+CE.
25、阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,请你用“等角对等边”的知识说明DE=BD+CE.