题目内容
【题目】如图,△ABC中,AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE. 求证:BD=CE.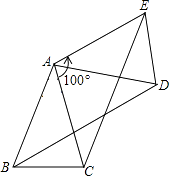
【答案】证明:∵△ABC绕点A按逆时针方向旋转100°得△ADE, ∴∠BAD=∠CAE=100°.
又∵AB=AC,
∴AB=AC=AD=AE.
在△ABD与△ACE中,
∵ 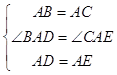 ,
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
【解析】先根据图形旋转的性质得出∠BAD=∠CAE=100°,再由SAS定理得出△ABD≌△ACE,由全等三角形的性质即可得出结论.
【考点精析】本题主要考查了等腰三角形的性质和旋转的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目