题目内容
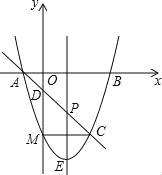
【题目】抛物线y=x2+bx+c与x轴交于点A（-1，0），B（3，0）两点，过点A的直线交抛物线于点C（2，m），交y轴于点D．
（1）求抛物线及直线AC的解析式；
（2）点P是线段AC上的一动点（点P与点A、C不重合），过点P作y轴的平行线交抛物线于点E，求线段PE长度的最大值；
（3）点M（m，-3）是抛物线上一点，问在直线AC上是否存在点F，使△CMF是等腰直角三角形？如果存在，请求出点F的坐标；如果不存在，请说明理由．
【答案】（1）y=x2-2x-3．y=-x-1．（2）
．（3）点F为（1，-2）.
【解析】
试题分析：（1）将A、B的坐标代入抛物线中，易求出抛物线的解析式；将C点横坐标代入抛物线的解析式中，即可求出C点的坐标，再由待定系数法可求出直线AC的解析式．
（2）PE的长实际是直线AC与抛物线的函数值的差，可设P点的横坐标为x，用x分别表示出P、E的纵坐标，即可得到关于PE的长、x的函数关系式，根据所得函数的性质即可求得PE的最大值．
（3）根据点F的不同位置分类讨论．
试题解析：（1）将A（-1，0），B（3，0）代入y=x2+bx+c，
得b=-2，c=-3；
∴y=x2-2x-3．
将C点的横坐标x=2代入y=x2-2x-3，
得y=-3，∴C（2，-3）；
∴直线AC的函数解析式是y=-x-1．
（2）设P点的横坐标为x（-1≤x≤2），
则P、E的坐标分别为：P（x，-x-1），E（x，x2-2x-3）；
∵P点在E点的上方，PE=（-x-1）-（x2-2x-3）=-x2+x+2，
=-（x-
）2+
∴当x=1/2时，PE的最大值=．
（3）①当点F在D点时，
将直线和抛物线的解析式组成方程组：
，
解得：
，
，
∴点C的坐标为（2，-3），
令x=0，y=x2-2x-3=-3，
∴M的坐标为（0，-3）
由直线的解析式可求点D的坐标为（0．-1）
∴MC=2，MD=3-1=2，
∵MC∥y轴，
∴∠CMD=90°，
即△CMD是等腰直角三角形，
∴当点F的坐标为（-1，0）时，△CMD是等腰直角三角形．
②当F在P点时，
当点E是顶点坐标时，可得PM=PC，
由抛物线的解析式可得对称轴为x=-1，
解方程组：
，解得
．
∴点P的坐标为（1，-2）
∴PC=MP=
，
又∵MC=2，
∴PC2+PM2=MC2，
由勾股定理的逆定理可得：△PMC为等腰直角三角形．
即△FMC为等腰直角三角形．
∴F点的坐标为（1，-2）．
③当F不在P、D点时，设点F（x，-x-1），
则CM=CF=
=2
即（x-2）2+（-x-3+3）2=4
解得：x1=2+
，x2=2-，
∴F（2+，-3-）或F（2-，-3+ ）．
当F（2+，-3-）时，FM=
，
∴CM2+CF2≠MF2，不能构成直角三角形，
同理：当F（2-，-3+ ）时，也不能构成直角三角形．
综上所述，存在点F为（1，-2）时．使△CMF是等腰直角三角形
