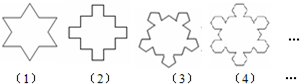
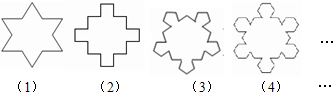
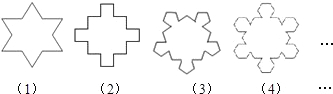
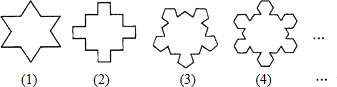
题目内容
如图,第(1)个多边形由正三角形“扩展“而来,边数记为a3,第(2)个多边形由正方形“扩展“而来,边数记为a4,…,依此类推,由正n边形“扩展“而来的多边形的边数记为an(n≥3).则a8的值是________.
解:(1)n=3时,边数为3×4=12;
n=4时,边数为4×5=20;
…
n=8时,边数为8×9=72;
∴a8=72.
故答案为:72.
分析:观察可得边数与扩展的正n边形的关系为n×(n+1),把n=8代入求解即可.
点评:本题考查了图形的规律性及规律性的应用;得到边数与扩展的正n边形的关系是解决本题的突破点.
n=4时,边数为4×5=20;
…
n=8时,边数为8×9=72;
∴a8=72.
故答案为:72.
分析:观察可得边数与扩展的正n边形的关系为n×(n+1),把n=8代入求解即可.
点评:本题考查了图形的规律性及规律性的应用;得到边数与扩展的正n边形的关系是解决本题的突破点.

练习册系列答案
相关题目