Question

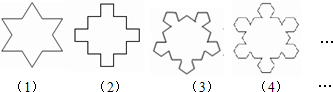
如图，第（1）个多边形由正三角形“扩展”而来，边数记为a₃，第（2）个多边形由正方形“扩展”而来，边数记为a₄，…以此类推，由正n边形“扩展”而来的多边形的边数记为a_n（n≥3），则a₆=

 

，当

1

a3

+…+

1

an

=

98

303

时，则n=

 

．

Answer 1

分析：首先分析题意及观察图形得到规律，一个正多边形“扩展”，即在原来正多变形的基础上，每个边再加上一个正多边形，由此可求出a₆，又可表示出a_n，再由已知求出n．

解答：解：由已知和图形，可知，
正三角形“扩展”，即在原来正三角形的基础上，每边再加上一个正三角形，
由此，a₆即由正六边形扩展而来，即在原来正六边形的基础上，每边再加上一个六边形，
即a₆的值为：6×（5+2）=42．
所以a_n=n（n+1），
所以

1

a3

+

1

a4

+…+

1

an

=

1

3×4

+

1

4×5

+…+

1

n(n+1)

=

1

3

-

1

4

+

1

4

-

1

5

+…+

1

n

-

1

n+1

=

1

3

-

1

n+1

=

98

303

，
所以n=100．
故答案分别为：42，100．

点评：此题考查的知识点是图形数字变化类问题，解题的关键是通过分析观察得出规律求出答案．