题目内容
【题目】如图，把正六边形各边按同一方向延长，使延长的线段与原正六边形的边长相等，顺次连接这六条线段外端点可以得到一个新的正六边形，…，重复上述过程，经过2018次后，所得到的正六边形边长是原正六边形边长的（ ）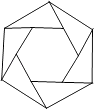 
A.（ 
）2016倍
B.（ 
）2017倍
C.（ ）2018倍
D.（ ）2019倍
【答案】C
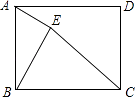
【解析】解：∵此六边形是正六边形， ∴∠1=180°﹣120°=60°，
∵AD=CD=BC，
∴△BCD为等边三角形，
∴BD= 
AC，
∴△ABC是直角三角形
又∵BC= AC，
∴∠2=30°，
∴AB= 
BC= CD，
同理可得，经过2次后，所得到的正六边形是原正六边形边长（ ）2倍，
∴经过2018次后，所得到的正六边形是原正六边形边长的（ ）2018 ，
故选C．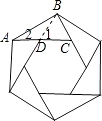
【考点精析】通过灵活运用正多边形和圆，掌握圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等即可以解答此题．
练习册系列答案
相关题目
【题目】先填写表，通过观察后再回答问题：
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
（1）表格中x= ，y= ；
（2）从表格中探究a与
数位的规律，并利用这个规律解决下面两个问题：
①已知
≈3.16，则
≈ ；
②已知
=8.973，若
=897.3，用含m的代数式表示b，则b= ；
（3）试比较与a的大小．
