题目内容
【题目】将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
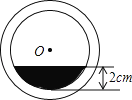
A.(![]() π﹣4
π﹣4![]() )cm2B.(
)cm2B.(![]() π﹣8
π﹣8![]() )cm2
)cm2
C.(![]() π﹣4
π﹣4![]() )cm2D.(
)cm2D.(![]() π﹣2
π﹣2![]() )cm2
)cm2
【答案】A
【解析】
作OD⊥AB于C,交小圆于D,则CD=2,由垂径定理可知AC=CB,利用正弦函数求得∠OAC=30°,进而求得∠AOB=120°,利用勾股定理即可求出AB的值,从而利用S扇形S△AOB求得杯底有水部分的面积.
解:作OD⊥AB于C,交小圆于D,则CD=2,AC=BC,
∵OA=OD=4,CD=2,
∴OC=2,
在Rt△AOC中,sin∠OAC=![]() =
=![]() ,
,
∴∠OAC=30°,
∴∠AOC=60°,
∴∠AOB=120°,AC=![]() ,
,
∴AB=![]() ,
,
∴杯底有水部分的面积=S扇形﹣S△AOB=![]() cm2,
cm2,
故选:A.

练习册系列答案
相关题目
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价.
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A、B两类图书共1000本 2.A类图书不少于600本 | |