题目内容
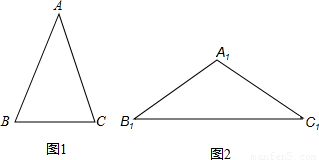
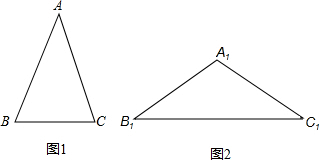
三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
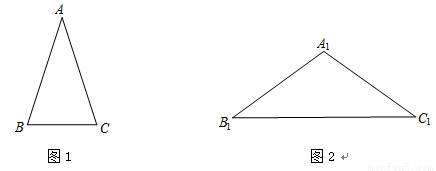
1.在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
2.△BCD是不是黄金三角形,如果是,请给出证明;如果不是,请说明理由;
3.设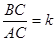 ,试求k的值;
,试求k的值;
4.如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,
请直接写出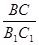 的值.
的值.
【答案】
1.如图所示
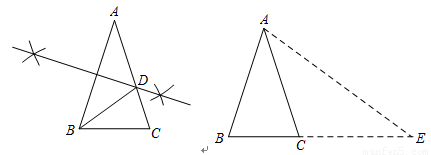
2.△BCD是黄金三角形.
证明如下:
∵点D在AB的垂直平分线上,
∴AD=BD,
∴∠ABD=∠A.
∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°,
∴∠ABD=∠DBC=36°.
又∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴△BCD是黄金三角形.
3.设BC=x,AC=y,
由(2)知,AD=BD=BC=x.
∵∠DBC=∠A,∠C=∠C,
∴△BDC∽△ABC,
∴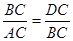 ,即
,即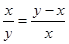 ,
,
整理,得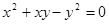 ,
,
解得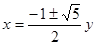 ./
./
因为x、y均为正数,所以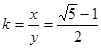 .
.
4.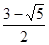
理由:延长BC到E,使CD=AC,连接AE.
∵∠A=36°,AB=AC,
∴∠ACB=∠B=72°,
∴∠ACE=180°-72°=108°,
∴∠ACE=∠B1A1C1.
∵A1B1=AB,
∴AC=CE=A1B1=A1C1,
∴△ACE≌△B1A1C1,
∴AE=B1C1.
由(3)知,,
∴ ,
,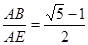 ,
,
∴ .
.
【解析】略

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目


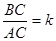 ,试求k的值;
,试求k的值; 的值.
的值.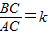 ,试求k的值;
,试求k的值;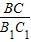 的值.
的值.