题目内容
已知等腰三角形底边长为8,腰长是方程x2-9x+20=0的一个根,求这个三角形的面积.
如下图所示:
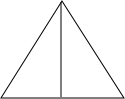
∵x2-9x+20=0,
(x-4)(x-5)=0,
∴x1=4,x2=5;
而等腰三角形底边长为8,
x=4时,4,4,8的三条线段不能组成三角形,
故腰长为x=5,
设高为h,由勾股定理得:
h=
=3,
∴高为3,
所以,三角形的面积为
×8×3=12.

∵x2-9x+20=0,
(x-4)(x-5)=0,
∴x1=4,x2=5;
而等腰三角形底边长为8,
x=4时,4,4,8的三条线段不能组成三角形,
故腰长为x=5,
设高为h,由勾股定理得:
h=
| 52-42 |
∴高为3,
所以,三角形的面积为
| 1 |
| 2 |

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目




 需要多少块地砖?
需要多少块地砖?