题目内容
【题目】如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
(1)说明AN=MB;
(2)将△ACM绕点C按逆时针旋转180°,使A点落在CB上,请对照原题图画出符合要求的图形;
(3)在(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由;若不成立,也请说明理由.

【答案】(1)详见解析;(2)详见解析;(3)成立,理由详见解析.
【解析】
(1)根据题意证明△ACN≌△MCB即可;
(2)本题考查了考生的画图能力以及空间想象能力;
(3)与(1)题相同,证明△ACN≌△BCM即可.
(1)∵三角形ACM以及三角形CBN为等边三角形,∴AC=CM,CN=CB,∠ACM=∠BCN,∴∠NCA=∠MCB,∴△ACN≌△MCB(SAS),∴AN=MB.
(2)如图,△A′M′C.
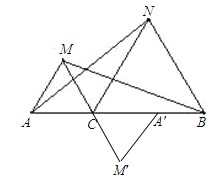
(3)∵△CBN与△ACM是等边三角形,∴BC=NC,CM=AC,∠NCB=∠MCA=60°,∴∠MCB=∠ACN,∴△CBM≌△CNA(SAS),∴AN=BM.

练习册系列答案
相关题目
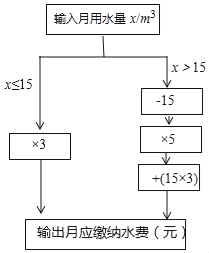
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.