题目内容
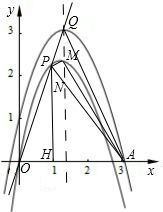
如图,已知在直角坐标平面内,点A的坐标为(3,0),第一象限内的点P在直线y=2x上,∠PAO=45度.
(1)求点P的坐标;
(2)如果二次函数的图象经过P、O、A三点,求这个二次函数的解析式,并写出它的图象的顶点坐标M;
(3)如果将第(2)小题中的二次函数的图象向上或向下平移,使它的顶点落在直线y=2x上的点Q处,求△APM与△APQ的面积之比.
分析:(1)根据题意设点P的坐标为(x,2x),又由∠PAO=45°,PH⊥OA,可得PH=AH=2x,又由点A的坐标为(3,0),即可求得x的值,则可求得点P的坐标;
(2)利用待定系数法将点P,O,A的坐标代入解析式即可得到方程组,解方程组即可求得解析式;
(3)根据图形求得:△APO、△AQO与四边形AMPO的面积,即可求得△APM与△APQ的面积,则问题得解.
(2)利用待定系数法将点P,O,A的坐标代入解析式即可得到方程组,解方程组即可求得解析式;
(3)根据图形求得:△APO、△AQO与四边形AMPO的面积,即可求得△APM与△APQ的面积,则问题得解.
解答:解:(1)过点P作PH⊥OA,垂足为点H.
∵点P在直线y=2x上,
∴设点P的坐标为(x,2x).
∵∠PAO=45°,PH⊥OA,
∴∠PAO=∠APH=45°.
∴PH=AH=2x.
∵点A的坐标为(3,0),
∴x+2x=3.
∴x=1.
∴点P的坐标为(1,2).
(2)设所求的二次函数解析式为y=ax2+bx+c(a≠0).
∵图象经过P(1,2)、O(0,0)、A(3,0)三点,
∴
,
解得
,
∴所求的二次函数解析式为y=-x2+3x.
顶点M的坐标为(
,
).
(3)根据题意,得点Q的坐标为(
,3).
∵S△AQO=
×3×3=
,
S△APO=
×3×2=3,
S四边形AMPO=
×1×2+
×(2+
)×
+
×
×
=
,
∴S△APM=
-3=
,S△APQ=
-3=
.
∴△APM与△APQ的面积之比为
.
另解:根据题意,得点Q的坐标为(
,3).
设图象的对称轴与直线AP相交于点N,则点N的坐标为(
,
).
∴MN=
-
=
,QN=3-
=
.
∴MN=
QN,
∴
=
,
=
.
∴△APM与△APQ的面积之比为
.
∵点P在直线y=2x上,
∴设点P的坐标为(x,2x).
∵∠PAO=45°,PH⊥OA,
∴∠PAO=∠APH=45°.
∴PH=AH=2x.
∵点A的坐标为(3,0),
∴x+2x=3.
∴x=1.
∴点P的坐标为(1,2).
(2)设所求的二次函数解析式为y=ax2+bx+c(a≠0).
∵图象经过P(1,2)、O(0,0)、A(3,0)三点,
∴
|
解得
|
∴所求的二次函数解析式为y=-x2+3x.
顶点M的坐标为(
| 3 |
| 2 |
| 9 |
| 4 |
(3)根据题意,得点Q的坐标为(
| 3 |
| 2 |
∵S△AQO=
| 1 |
| 2 |
| 9 |
| 2 |
S△APO=
| 1 |
| 2 |
S四边形AMPO=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 15 |
| 4 |

∴S△APM=
| 15 |
| 4 |
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 2 |
∴△APM与△APQ的面积之比为
| 1 |
| 2 |
另解:根据题意,得点Q的坐标为(
| 3 |
| 2 |
设图象的对称轴与直线AP相交于点N,则点N的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
∴MN=
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
∴MN=
| 1 |
| 2 |
∴
| S△PMN |
| S△PQN |
| 1 |
| 2 |
| S△AMN |
| S△AQN |
| 1 |
| 2 |
∴△APM与△APQ的面积之比为
| 1 |
| 2 |
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法以及三角形面积的求法等知识点.主要考查学生数形结合的数学思想方法.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目