题目内容
如图,大坝的横截面是一个梯形,坝顶宽DC=10m,坝高15m,斜坡A的坡度l1=1:2,斜坡BC的坡度l2=3:4,则坡底宽AB= m.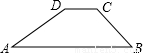
【答案】分析:过D,C作AB的垂线,在直角三角形中求直角边,进而可得AB边的长.
解答: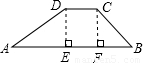 解:如图所示,过D,C作AB的垂线,垂足分别为E,F
解:如图所示,过D,C作AB的垂线,垂足分别为E,F
由题意可得DE=15.
∵斜坡A的坡度l1=1:2,
∴DE:AE=1:2,
∴AE=30.
∵斜坡BC的坡度l2=3:4,
∴CF:BF=3:4,
∴BF=20.
∴AB=AE+EF+FB=30+10+20=60(m).
点评:考查了坡度的定义及其与坡角的关系.
解答:
 解:如图所示,过D,C作AB的垂线,垂足分别为E,F
解:如图所示,过D,C作AB的垂线,垂足分别为E,F由题意可得DE=15.
∵斜坡A的坡度l1=1:2,
∴DE:AE=1:2,
∴AE=30.
∵斜坡BC的坡度l2=3:4,
∴CF:BF=3:4,
∴BF=20.
∴AB=AE+EF+FB=30+10+20=60(m).
点评:考查了坡度的定义及其与坡角的关系.

练习册系列答案
相关题目
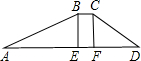 如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡度i=1:2.5(i为坡比),斜坡CD的坡度i=1:2,求坝底宽AD.
如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡度i=1:2.5(i为坡比),斜坡CD的坡度i=1:2,求坝底宽AD. 11、如图,大坝的横截面是一个梯形,坝顶宽DC=10m,坝高15m,斜坡A的坡度l1=1:2,斜坡BC的坡度l2=3:4,则坡底宽AB=
11、如图,大坝的横截面是一个梯形,坝顶宽DC=10m,坝高15m,斜坡A的坡度l1=1:2,斜坡BC的坡度l2=3:4,则坡底宽AB=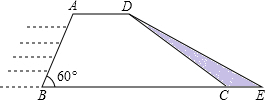
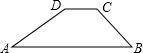 如图,大坝的横截面是一个梯形,坝顶宽DC=10m,坝高15m,斜坡A的坡度l1=1:2,斜坡BC的坡度l2=3:4,则坡底宽AB=________m.
如图,大坝的横截面是一个梯形,坝顶宽DC=10m,坝高15m,斜坡A的坡度l1=1:2,斜坡BC的坡度l2=3:4,则坡底宽AB=________m.