题目内容
《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.(参考数据:
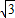 ≈1.73,sin27°≈0.45,cos27°≈0.89,tan27°≈0.50)
≈1.73,sin27°≈0.45,cos27°≈0.89,tan27°≈0.50)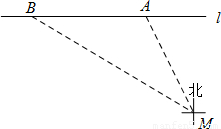
【答案】分析:首先过M作MC⊥AB于C,根据题意得:∠MBC=27°,∠MAC=60°,CM=90m,然后利用三角函数中的正切函数,求得BC与AC的值,继而可求得此车从A到B的平均速度,比较19.44m/s,即可确定此车是否超过限速.
解答: 解:过M作MC⊥AB于C,
解:过M作MC⊥AB于C,
根据题意得:∠AMC=27°,∠BMC=60°,CM=90m,
在Rt△ACM中,AC=CM•tan27°≈90×0.50=45(m),
在Rt△BCM中,BC=CM•tan60°=90×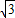 ≈90×1.73=155.7(m),
≈90×1.73=155.7(m),
∴AB=BC-AC=110.7(m),
∵此车从点A行驶到点B所用的时间为6s,
∴此车从A到B的平均速度为:110.7÷6≈18.45(m/s)<19.44m/s.
∴此车从A到B的平均速度为18.43m/s,此车不超限速.
点评:此题考查了方向角问题.此题难度适中,解此题的关键是利用三角函数解直角三角形.
解答:
 解:过M作MC⊥AB于C,
解:过M作MC⊥AB于C,根据题意得:∠AMC=27°,∠BMC=60°,CM=90m,
在Rt△ACM中,AC=CM•tan27°≈90×0.50=45(m),
在Rt△BCM中,BC=CM•tan60°=90×
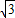 ≈90×1.73=155.7(m),
≈90×1.73=155.7(m),∴AB=BC-AC=110.7(m),
∵此车从点A行驶到点B所用的时间为6s,
∴此车从A到B的平均速度为:110.7÷6≈18.45(m/s)<19.44m/s.
∴此车从A到B的平均速度为18.43m/s,此车不超限速.
点评:此题考查了方向角问题.此题难度适中,解此题的关键是利用三角函数解直角三角形.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
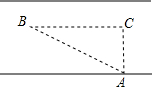 “中华人民共和国道路管理条例”规定:小汽车在城市街路上的行驶速度不得超过70千米/时.一辆小汽车在一条城市街路上直道行驶时,某一时刻刚好行驶到路对面车速检测仪观测点A正前方50米的C处,过了6秒后,行驶到B处的小汽车与车速检测仪间的距离变为130米,请你判断这辆小汽车是否超速?
“中华人民共和国道路管理条例”规定:小汽车在城市街路上的行驶速度不得超过70千米/时.一辆小汽车在一条城市街路上直道行驶时,某一时刻刚好行驶到路对面车速检测仪观测点A正前方50米的C处,过了6秒后,行驶到B处的小汽车与车速检测仪间的距离变为130米,请你判断这辆小汽车是否超速? 27、“中华人民共和国道路交通管理条例”规定:小汽车在高速公路上的行驶速度不得超过120千米/时.一辆小汽车在一条高速公路上直道行驶,某一时刻刚好行驶到“车速检测点A”正前方50米C处,过了4秒后,测得小汽车位置B与“车速检测点A”之间的距离为130米,这辆小汽车超速了吗?请说明理由.
27、“中华人民共和国道路交通管理条例”规定:小汽车在高速公路上的行驶速度不得超过120千米/时.一辆小汽车在一条高速公路上直道行驶,某一时刻刚好行驶到“车速检测点A”正前方50米C处,过了4秒后,测得小汽车位置B与“车速检测点A”之间的距离为130米,这辆小汽车超速了吗?请说明理由.
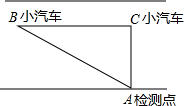 “中华人民共和国道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直通行驶到车速检测仪A的正前方50米C处,过了4秒后行驶到B处,此时测得小汽车与车速检测仪A之间距离为130米,这辆小汽车超速了吗?
“中华人民共和国道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直通行驶到车速检测仪A的正前方50米C处,过了4秒后行驶到B处,此时测得小汽车与车速检测仪A之间距离为130米,这辆小汽车超速了吗? “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过25米/秒,如图,一辆汽车在一条城市街路上沿东西方向行驶,某一时刻刚好行驶到距车速检测仪A点距离为40米的C(位于A点北偏东30°处)处,过了3秒钟,到达B点,(位于A点北偏西45°)此时小汽车距车速检测仪间的距离为60米,那么这辆汽车是否超速?
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过25米/秒,如图,一辆汽车在一条城市街路上沿东西方向行驶,某一时刻刚好行驶到距车速检测仪A点距离为40米的C(位于A点北偏东30°处)处,过了3秒钟,到达B点,(位于A点北偏西45°)此时小汽车距车速检测仪间的距离为60米,那么这辆汽车是否超速?