题目内容
【题目】(1)分解因式: ![]() ;
;
(2)解下列不等式组,并求出该不等式组的自然数解之和.
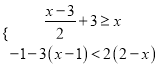
【答案】(1)![]()
(2)原不等式组的解集是-2<x≤3
自然数解之和为:0+1+2+3=6
【解析】试题分析:
(1) 观察式子的形式可以看出各项均有公因式2a,可用提公因式法分解;提出公因式后发现其中的一个式子的形式符合完全平方公式,可用公式法进一步分解因式.
(2) 将组成该不等式组的每一个不等式分别解出,再利用数轴表示出各不等式的解集,最后选取各解集的公共部分;至于自然数解,可在求出的不等式解集中依次寻找.
试题解析:
(1) 2a3-8a2+8a=2a(a2-4a+4)=2a(a-2)2.
(2) 先解第一个不等式:
![]() ,
,
去分母,得 (x-3)+6≥2x,
去括号,得 x-3+6≥2x,
移项,得 x-2x≥-6+3,
合并同类项,得 -x≥-3,
系数化为1,得 x≤3.
再解第二个不等式:
-1-3(x-1)<2(2-x),
去括号,得 -1-3x+3<4-2x,
移项,得 -3x+2x<4-3+1,
合并同类项,得 -x<2,
系数化为1,得 x>-2.
在数轴上表示解集:
![]()
故该不等式组的解集为:-2<x≤3.
该不等式组的自然数解有:0,1,2,3,自然数解之和为0+1+2+3=6.

【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为![]() .
.
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.