题目内容
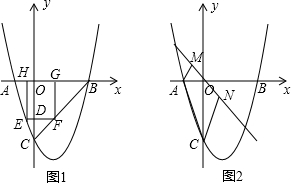 (2013•黄陂区模拟)已知:抛物线y=x2+mx+n的顶点D(1,-4)抛物线与坐标轴的交点为A,B,C,
(2013•黄陂区模拟)已知:抛物线y=x2+mx+n的顶点D(1,-4)抛物线与坐标轴的交点为A,B,C,(1)求抛物线的解析式,并求出A,B,C,的坐标;
(2)作如图所示四个顶点在△ABC三边上的矩形EFGH.求矩形EFGH的最大面积;
(3)MN=
| 2 |
分析:(1)由抛物线y=x2+mx+n的顶点为D(1,-4),根据二次函数的性质可得其顶点式为y=(x-1)2-4,展开即得抛物线的解析式为y=x2-2x-3;令y=0时,解方程x2-2x-3=0,可得与x轴的交点A与B的坐标,令x=0,可得与y轴交点C的坐标;
(2)如题目图1,设G(p,0),H(q,0),运用待定系数法求出直线AC的解析式为y=-3x-3,直线BC的解析式为y=x-3,则E(q,-3q-3),F(p,p-3),根据矩形的性质得EF∥x轴,得p-3=-3q-3,则p=-3q,再用含q的代数式分别表示GH,GF,根据矩形面积公式得出矩形EFGH的面积=-12(q+
)2+3,然后由二次函数的性质即可求出矩形EFGH的最大面积;
(3)由于四边形AMNC的周长=AM+MN+NC+CA,而MN=
,CA=
,为定值,所以当AM+NC的和最小时,四边形AMNC的周长最小.为此,取D1(0,-1)得?AMND,则AM=DN,作D关于直线y=-x的对称点交x轴于点D′(1,0),连接CD′交直线y=-x于点N,此时AM+NC=ND1+NC=NC+ND′=CD′时最小.运用待定系数法求出直线CD′的解析式,再与y=-x联立组成方程组,即可求出点N的坐标.
(2)如题目图1,设G(p,0),H(q,0),运用待定系数法求出直线AC的解析式为y=-3x-3,直线BC的解析式为y=x-3,则E(q,-3q-3),F(p,p-3),根据矩形的性质得EF∥x轴,得p-3=-3q-3,则p=-3q,再用含q的代数式分别表示GH,GF,根据矩形面积公式得出矩形EFGH的面积=-12(q+
| 1 |
| 2 |
(3)由于四边形AMNC的周长=AM+MN+NC+CA,而MN=
| 2 |
| 10 |
解答:解:(1)∵抛物线y=x2+mx+n的顶点为D(1,-4),
∴抛物线的顶点式为y=(x-1)2-4,即为y=x2-2x-3,
当y=0时,x2-2x-3=0,解得x=-1或3,即A点坐标为(-1,0),B点坐标为(3,0),
当x=0时,y=-3,即C点坐标为(0,-3);
(2)如题目图1,设G点坐标为(p,0),H点坐标为(q,0).
易求直线AC的解析式为y=-3x-3,直线BC的解析式为y=x-3,
∴E点坐标为(q,-3q-3),F点坐标为(p,p-3),
∵矩形EFGH中,EF∥HG,
∴p-3=-3q-3,∴p=-3q,
∴GH=p-q=-4q,GF=|p-3|=3-p=3+3q,
∴矩形EFGH的面积=GH•GF=-4q(3+3q)=-12q2-12q=-12(q+
)2+3,
∴当q=-
时,矩形EFGH的面积最大,最大面积为3;
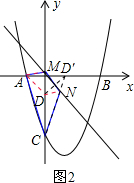 (3)取D1(0,-1),连接AD1,则AD1=MN=
(3)取D1(0,-1),连接AD1,则AD1=MN=
,AD1∥MN,
∴四边形AMND1是平行四边形,AM=DN.
在x轴上取点D′(1,0),连接CD′交直线MN:y=-x于点N,则DO=D′O=1,∠D1ON=∠D′ON=45°,
∴MN是线段D1D′的垂直平分线,即D1与D′关于直线MN对称,
∴ND1=ND′,
∴AM+NC=ND1+NC=ND′+NC=CD′最小,则四边形AMNC的周长最小.
运用待定系数法求出直线CD′的解析式为y=3x-3,
由
,解得
,
∴N的坐标为(
,-
).
∴抛物线的顶点式为y=(x-1)2-4,即为y=x2-2x-3,
当y=0时,x2-2x-3=0,解得x=-1或3,即A点坐标为(-1,0),B点坐标为(3,0),
当x=0时,y=-3,即C点坐标为(0,-3);
(2)如题目图1,设G点坐标为(p,0),H点坐标为(q,0).
易求直线AC的解析式为y=-3x-3,直线BC的解析式为y=x-3,
∴E点坐标为(q,-3q-3),F点坐标为(p,p-3),
∵矩形EFGH中,EF∥HG,
∴p-3=-3q-3,∴p=-3q,
∴GH=p-q=-4q,GF=|p-3|=3-p=3+3q,
∴矩形EFGH的面积=GH•GF=-4q(3+3q)=-12q2-12q=-12(q+
| 1 |
| 2 |
∴当q=-
| 1 |
| 2 |
 (3)取D1(0,-1),连接AD1,则AD1=MN=
(3)取D1(0,-1),连接AD1,则AD1=MN=| 2 |
∴四边形AMND1是平行四边形,AM=DN.
在x轴上取点D′(1,0),连接CD′交直线MN:y=-x于点N,则DO=D′O=1,∠D1ON=∠D′ON=45°,
∴MN是线段D1D′的垂直平分线,即D1与D′关于直线MN对称,
∴ND1=ND′,
∴AM+NC=ND1+NC=ND′+NC=CD′最小,则四边形AMNC的周长最小.
运用待定系数法求出直线CD′的解析式为y=3x-3,
由
|
|
∴N的坐标为(
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题是二次函数的综合题型,其中涉及到抛物线的顶点式,二次函数的最值,二次函数图象上点的坐标特征,运用待定系数法求直线的解析式,矩形的面积,轴对称-最短路线问题,函数图象交点的求法等知识.运用数形结合、方程思想是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
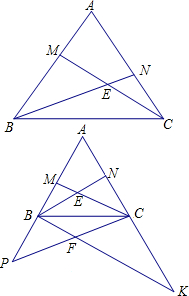 (2013•黄陂区模拟)正△ABC的两边上的点M,N满足BM=AN,BN交于CN于点E
(2013•黄陂区模拟)正△ABC的两边上的点M,N满足BM=AN,BN交于CN于点E