题目内容
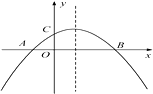
【题目】如图，两直线l1：y＝kx﹣2b+1和l2：y＝（1﹣k）x+b﹣1交于x轴上一点A，与y轴分别交于点B、C，若A的横坐标为2.
（1）求这两条直线的解析式；
（2）求△ABC的面积．
【答案】（1）y＝
x﹣3，y＝﹣
x+1；（2）4
【解析】
（1）把A点坐标分别代入y=kx-2b+1和y=（1-k）x+b-1得到关于k、b的方程组，然后解方程组即可确定这两条直线的解析式；
（2）先根据（1）中的解析式确定B点和C点坐标，然后根据三角形面积公式求解．
解：（1）把A（2，0）分别代入y＝kx﹣2b+1和y＝（1﹣k）x+b﹣1得：
，解得
，
所以直线l1的解析式为y＝x﹣3，直线l2的解析式为y＝﹣x+1；
（2）当x＝0时，y＝x﹣3＝﹣3，则B点坐标为（0，﹣3）；当x＝0时，y＝﹣x+1＝1，则C点坐标为（0，1），
∴△ABC的面积＝×（1+3）×2＝4．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
【题目】鲁能巴蜀中学2018年校艺术节“巴蜀好声音”独唱预选赛中，初二年级25名同学的成绩
满分为10分
统计如下：
，
，
，
，
，
，
，
，
，
，
，
，
，，，
，
，
，
，
，
，，
，
，10
分及以上为A级，
分为B级包括分和
分，
分为C级包括分和分，分以下为D级
请把下面表格补充完整；
等级 | A | B | C | D |
人数 | 4 | 8 |
级8位同学成绩的中位数是多少，众数是多少；
若成绩为A级的同学将参加学校的汇演，请求出初二年级A级同学的平均成绩？
