Question

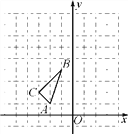
【题目】如图，一次函数y=kx+5(k为常数，且k≠0)的图像与反比例函数y=-的函数交于A、B(4，b)两点.

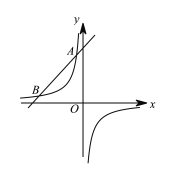
(1)求一次函数的表达式及A点的坐标；

(2)直接写出一次函数的值大于反比例函数的值时，自变量x的取值范围.

Answer 1

【答案】（1）y=x+5，A(1，4)（2）4＜x＜1或x＞0

【解析】

（1）先利用反比例函数求出b=1，得到B点坐标为（-4，1），然后把B点坐标代入y=kx+5中求出k，从而得到一次函数解析式，联立反比例函数和一次函数解析式，解方程组即可求得点A的值；

（2）根据A、B的坐标结合图象即可求出答案．

（1）把B(4，b)代入y=得b=1，

所以B点坐标为(4，1)，

把B(4，1)代入y=kx+5得4k+5=1，解得k=1，

所以一次函数解析式为y=x+5；

解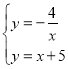得或

∴A(1，4)，

（2）∵两函数的交点A的坐标是(1，4)，B的坐标是(4，1)，

∴一次函数值大于反比例函数值时自变量x的取值范围是4＜x＜1或x＞0.