题目内容
【题目】如图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是![]() 的中点,AB和DC的延长线交于⊙O外一点E.
的中点,AB和DC的延长线交于⊙O外一点E.
求证:(1)∠EBC=∠D;
(2)BC=EC.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据圆内接四边形的性质可知:∠ABC+∠D=180°,而∠ABC+∠EBC=180°,从而可以证明∠EBC=∠D;
(2)连接AC,先根据直径所对的角是直角,圆内接四边形的性质和等弧所对的圆周角相等得到∠E=∠D,∠EBC=∠E,从而根据等角对等边可证BC=EC.
证明:(1)∵四边形ABCD内接于⊙O,
∴∠ABC+∠D=180°.
又∵∠ABC+∠EBC=180°,
∴∠EBC=∠D.
(2)如图,连结AC.
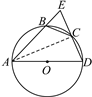
∵AD是⊙O的直径,
∴∠ACD=90°,
∵C是![]() 的中点,∴∠EAC=∠CAD,
的中点,∴∠EAC=∠CAD,
而∠EAC与∠E互余,∠CAD与∠D互余,
∴∠E=∠D,由(1)得∠EBC=∠D,
∴∠EBC=∠E,∴BC=EC.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目