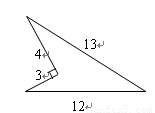
题目内容
 有一块田地的形状和尺寸如图所示∠B=∠D=90°,∠A=60°,AB=5米,AD=4米,试求它的面积.
有一块田地的形状和尺寸如图所示∠B=∠D=90°,∠A=60°,AB=5米,AD=4米,试求它的面积.分析:首先延长DC交AB延长线于E,构造直角三角形,根据∠A=60°可得∠E=30°,根据直角三角形的性质可以得到AE=2AD,从而得到AE的长,再根据勾股定理求出DE的长,进而算出△ADE的面积,由AE、AB的长求出BE的长,再利用勾股定理算出CB的长,可以得到△BCE的面积,用△ADE的面积-△BCE的面积可得到这块地的面积.
解答: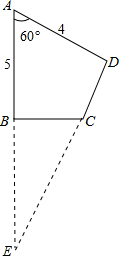 解:延长DC交AB延长线于E,
解:延长DC交AB延长线于E,
∵∠D=90°,∠A=60°,
∴∠E=180°-90°-60°=30°,
∴AE=2AD=8米,
∴DE=
=
=
=4
(米),
则S△ADE=
•AD•DE=
×4×4
=8
(平方米)
∵AB=5米,
∴BE=8-5=3(米),
∵∠ABC=90°,
∴∠CBE=90°,
设CB=x米,则CE=2x米,
x2+32=(2x)2,
解得:x=
,
则S△CBE=
CB•EB=
×
×3=
(平方米),
∴这一块田地的面积是:S△ADE-S△CBE=8
-
=
(平方米),
答:这一块田地的面积是
平方米.
 解:延长DC交AB延长线于E,
解:延长DC交AB延长线于E,∵∠D=90°,∠A=60°,
∴∠E=180°-90°-60°=30°,
∴AE=2AD=8米,
∴DE=
| AE2-AD2 |
| 64-16 |
| 48 |
| 3 |
则S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵AB=5米,
∴BE=8-5=3(米),
∵∠ABC=90°,
∴∠CBE=90°,
设CB=x米,则CE=2x米,
x2+32=(2x)2,
解得:x=
| 3 |
则S△CBE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∴这一块田地的面积是:S△ADE-S△CBE=8
| 3 |
3
| ||
| 2 |
13
| ||
| 2 |
答:这一块田地的面积是
13
| ||
| 2 |
点评:此题主要考查了勾股定理的应用,关键是正确作出辅助线,构造直角三角形,求出△ADE的面积和△BCE的面积.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,有一块田地的形状和尺寸如图所示,则它的面积为
如图,有一块田地的形状和尺寸如图所示,则它的面积为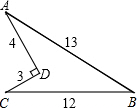 有一块田地的形状和尺寸如图所示,求它的面积.
有一块田地的形状和尺寸如图所示,求它的面积. 有一块田地的形状和尺寸如图所示,则它的面积为
有一块田地的形状和尺寸如图所示,则它的面积为