题目内容
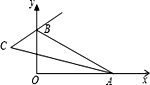
【题目】如图,在四边形 ![]() 中,
中, ![]() ,对角线
,对角线 ![]() 平分
平分 ![]() .
.
(1)求证: ![]() .
.
(2)若 ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)解:如图,

过 ![]() 点作
点作 ![]() ,
, ![]() ,
,
∵ ![]() 是
是 ![]() 的角平分线,
的角平分线,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]()
![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]() .
.
(2)解:∵ ![]() 且
且 ![]() 和
和 ![]() 为直角三角形,
为直角三角形,
∴设 ![]() ,
,
则 ![]() ,
, ![]() ,
,
而又∵ ![]() ≌
≌ ![]() ,
, ![]() ≌
≌ ![]() ,
,
∴ ![]() ,
,
即 ![]() ,解得
,解得 ![]() ,
,
∴ ![]() ,
,
则 ![]() 的长为
的长为 ![]()
【解析】(1)抓住已知条件AC平分 ∠B AD, 过C点作CE⊥AB , CF⊥AD,可证得CE=CF,再根据BC=CD,就可证明△CFD ≌ △CEB,得出∠D=∠EBC,然后根据∠EBC+∠B=180° ,即可证得结论。
(3)根据已知条件易证△BEC 和 △FDC 为等腰直角三角形,设它们的直角边长为x,就可表示出AE、AF的长,再根据全等三角形的性质证得AE=AF,建立关于x的方程,求出x的值,然后根据勾股定理,在Rt△ACF中就可求出AC的长。
【考点精析】通过灵活运用角平分线的性质定理和勾股定理的概念,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目