题目内容
已知:如图,⊙O的直径AB=8cm,P是AB延长线上的一点,过点P作⊙O的切线,切点为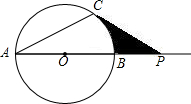 C,连接AC.
C,连接AC.(1)若∠ACP=120°,求阴影部分的面积;
(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M,∠CMP的大小是否发生变化若变化,请说明理由;若不变,求出∠CMP的度数.
分析:解:(1)连接OC.PC为⊙O的切线,由切线的性质知,∠PCO=90度.由已知∠ACP=120°,则有∠ACO=∠ACP-∠OCP=30°,由等边对等角知,∠A=∠ACO=30度.由三角形的外角等于与它不相邻的两个内角和知,∠BOC=60°,由正切的概念知PC=OCtan60°=4
,则阴影部分的面积可由△OCP的面积减去扇形OCB的面积.
(2)由(1)知∠BOC+∠OPC=90°,由角的平分线的性质知∠APM=
∠APC,由圆周角定理知,∠A=
∠BOC,
∴∠PMC=∠A+∠APM=
(∠BOC+∠OPC)=45°.
| 3 |
(2)由(1)知∠BOC+∠OPC=90°,由角的平分线的性质知∠APM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PMC=∠A+∠APM=
| 1 |
| 2 |
解答:解:(1)连接OC.
∵PC为⊙O的切线,
∴PC⊥OC.
∴∠PCO=90度.
∵∠ACP=120°
∴∠ACO=30°
∵OC=OA,
∴∠A=∠ACO=30度.
∴∠BOC=60°
∵OC=4
∴PC=4•tan60°=4
∴S阴影=S△OPC-S扇形BOC=8
-
;
(2)∠CMP的大小不变,∠CMP=45°
由(1)知∠BOC+∠OPC=90°
∵PM平分∠APC
∴∠APM=
∠APC
∵∠A=
∠BOC
∴∠PMC=∠A+∠APM=
(∠BOC+∠OPC)=45°.
∵PC为⊙O的切线,
∴PC⊥OC.
∴∠PCO=90度.
∵∠ACP=120°
∴∠ACO=30°
∵OC=OA,
∴∠A=∠ACO=30度.
∴∠BOC=60°
∵OC=4
∴PC=4•tan60°=4
| 3 |
∴S阴影=S△OPC-S扇形BOC=8
| 3 |
| 8π |
| 3 |
(2)∠CMP的大小不变,∠CMP=45°
由(1)知∠BOC+∠OPC=90°
∵PM平分∠APC
∴∠APM=
| 1 |
| 2 |
∵∠A=
| 1 |
| 2 |
∴∠PMC=∠A+∠APM=
| 1 |
| 2 |
点评:本题利用了切线的性质,等边对等角,三角形的外角与内角的关系,角的平分线的性质,正切的概念,三角形和扇形的面积公式求解.

练习册系列答案
相关题目
 窗户B,这时PA平分∠BPC.若点P到大楼的水平距离PC为10米.
窗户B,这时PA平分∠BPC.若点P到大楼的水平距离PC为10米. (2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12. 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.