题目内容
如图,已知矩形OABC,点P在边OA上(不与端点重合),点Q在边CO上(不与端点重合).(1)如图(1),若∠BPQ=90°,且△OPQ与△PAB和△QPB相似,请写出表示这三个三角形相似的式子,并探究此时线段OQ、QB、BA之间的数量关系.
(2)若∠PQB=90°,且△OPQ与△PAB、△QPB都相似,如图(2),请重新写出表示这三个三角形相似的式子,并证明AB:OA=2
 :3.
:3.(3)在(1)中,若OA=8
 ,OC=8,OP=
,OC=8,OP= CQ.以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴,建立平面直角坐标系,如图(3),若某抛物线顶点为P,点B在抛物线上.
CQ.以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴,建立平面直角坐标系,如图(3),若某抛物线顶点为P,点B在抛物线上.①求此抛物线的解析式.
②过线段BP上一动点M(点M与点P、B不重合),作y轴的平行线交抛物线于点N,若记点M的横坐标为m,试求线段MN的长L与m之间的函数关系式,画出该函数的示意图,并指出m取何值时,L有最大值,最大值是多少?

【答案】分析:(1)要写成三个三角形相似的式子,需要先找出相等的对应角,首先由BC∥OA,确定∠CBP=∠BPA>∠QBP,那么三个相似三角形的一组对应角应该是:∠QBP、∠QPO、∠ABP,显然能得出∠QBP=∠ABP、∠OQP=∠BQP,那么过P作BQ的垂线,根据角平分线定理即可判断出OQ、QB、BA三者之间的数量关系.
(2)同(1),先根据图示确定相似三角形的对应角,然后根据三个三角形的对应顶点写出三角形相似的式子;在△BQP、△BPA中,有公共边BP,可确定两者全等,那么BQ=AB,因此确定出∠CBQ的度数,即可确定AB、BC(OA)的比例关系,那么可以从△OQP、△CQB、△ABP这三个相似三角形入手.
(3)①首先结合(1)的解题过程,确定OP的长,进而得出点P的坐标,再利用待定系数法确定抛物线的解析式;
②首先利用待定系数法求出直线BP的解析式,然后根据直线BP、抛物线的解析式,用点M的横坐标表示出点M、N的纵坐标,两点纵坐标的差即为L的函数表达式,再根据函数的性质进行判断即可.
解答: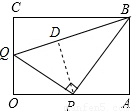 解:(1)△OPQ和△ABP中,∵∠OPQ+∠APB=90°,且∠APB+∠ABP=90°,
解:(1)△OPQ和△ABP中,∵∠OPQ+∠APB=90°,且∠APB+∠ABP=90°,
∴∠OPQ=∠ABP;
△BPQ和△ABP中,∵BC∥OA,∴∠APB=∠CBP>∠PBQ,
若两个三角形相似,则:∠PBQ=∠ABP;
∴∠OPQ=∠ABP=∠PBQ
又∵∠O=∠A=∠QPB=90°,
∴△OPQ∽△ABP∽△PBQ.
在△OPQ和△PBQ中,∠OQP=∠PQB,过P作PD⊥BQ于D,则 OQ=QD;
同理,可得:BD=AB,
∴BQ=QD+BD=OQ+AB.
(2)同(1)可确定∠QBP=∠ABP,由图知:∠QPO=∠BPA
∴∠OQP=∠ABP=∠QBP,又∠BQP=∠QOP=∠BAP=90°
∴△OPQ∽△APB∽△QPB.
由(1)的结论知:∠OQP=∠QBC=∠QBP=∠ABP,且∠ABC=90°,
∴∠QBC=30°,则 BQ:CB=2: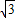 =2
=2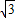 :3;
:3;
由△QPB∽△APB,且BP=BP,所以△QPB≌△APB,得:AB=BQ;
∴AB:BC=2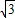 :3,即 AB:OA=2
:3,即 AB:OA=2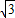 :3.
:3.
(3)①由(1)的解答过程知:若△OPQ与△PAB和△QPB相似,则必须满足的条件是∠QPB=90゜;
此时∠OQP=∠BQP、∠QBP=∠ABP,由(1)题图可知:OP=AP=PD;
∴OP=AP= OA=4
OA=4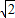 ,即 P(4
,即 P(4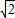 ,0);
,0);
设抛物线的解析式为:y=a(x-4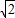 )2,代入点B(8
)2,代入点B(8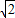 ,8),得:
,8),得:
a(8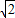 -4
-4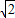 )2=8,解得 a=
)2=8,解得 a=
∴抛物线的解析式为:y= (x-4
(x-4 )2=
)2= x2-2
x2-2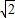 x+8.
x+8.
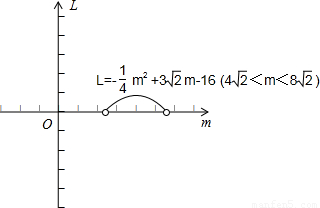 ②设直线BP的解析式为:y=kx+b,代入B(8
②设直线BP的解析式为:y=kx+b,代入B(8 ,8)、P(4
,8)、P(4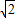 ,0),得:
,0),得:
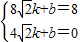 ,解得
,解得 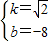
∴直线BP:y=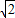 x-8.
x-8.
已知点M的横坐标为m,则 M(m,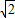 m-8)、N(m,
m-8)、N(m, m2-2
m2-2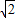 m+8),则有:
m+8),则有:
MN的长:L=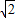 m-8-(
m-8-( m2-2
m2-2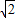 m+8)=-
m+8)=- m2+3
m2+3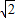 m-16(4
m-16(4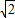 <m<8
<m<8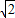 )(如右图)
)(如右图)
配方,得:L=- (m2-12
(m2-12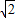 m+72)+2=-
m+72)+2=- (m-6
(m-6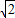 )2+2,
)2+2,
∴当m取6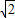 时,L有最大值,且最大值为 2.
时,L有最大值,且最大值为 2.
点评:此题主要考查的是相似三角形以及二次函数的相关知识,题目的难度逐题递进,前面的题目为后面的解答过程提供了很好的铺垫,这样也降低了解题的难度.在解题时,一定要注意合理利用图形的辅助作用.另外,在求函数解析式和画函数图象时,要注意自变量的取值范围.
(2)同(1),先根据图示确定相似三角形的对应角,然后根据三个三角形的对应顶点写出三角形相似的式子;在△BQP、△BPA中,有公共边BP,可确定两者全等,那么BQ=AB,因此确定出∠CBQ的度数,即可确定AB、BC(OA)的比例关系,那么可以从△OQP、△CQB、△ABP这三个相似三角形入手.
(3)①首先结合(1)的解题过程,确定OP的长,进而得出点P的坐标,再利用待定系数法确定抛物线的解析式;
②首先利用待定系数法求出直线BP的解析式,然后根据直线BP、抛物线的解析式,用点M的横坐标表示出点M、N的纵坐标,两点纵坐标的差即为L的函数表达式,再根据函数的性质进行判断即可.
解答:
 解:(1)△OPQ和△ABP中,∵∠OPQ+∠APB=90°,且∠APB+∠ABP=90°,
解:(1)△OPQ和△ABP中,∵∠OPQ+∠APB=90°,且∠APB+∠ABP=90°,∴∠OPQ=∠ABP;
△BPQ和△ABP中,∵BC∥OA,∴∠APB=∠CBP>∠PBQ,
若两个三角形相似,则:∠PBQ=∠ABP;
∴∠OPQ=∠ABP=∠PBQ
又∵∠O=∠A=∠QPB=90°,
∴△OPQ∽△ABP∽△PBQ.
在△OPQ和△PBQ中,∠OQP=∠PQB,过P作PD⊥BQ于D,则 OQ=QD;
同理,可得:BD=AB,
∴BQ=QD+BD=OQ+AB.
(2)同(1)可确定∠QBP=∠ABP,由图知:∠QPO=∠BPA
∴∠OQP=∠ABP=∠QBP,又∠BQP=∠QOP=∠BAP=90°
∴△OPQ∽△APB∽△QPB.
由(1)的结论知:∠OQP=∠QBC=∠QBP=∠ABP,且∠ABC=90°,
∴∠QBC=30°,则 BQ:CB=2:
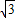 =2
=2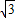 :3;
:3;由△QPB∽△APB,且BP=BP,所以△QPB≌△APB,得:AB=BQ;
∴AB:BC=2
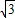 :3,即 AB:OA=2
:3,即 AB:OA=2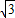 :3.
:3.(3)①由(1)的解答过程知:若△OPQ与△PAB和△QPB相似,则必须满足的条件是∠QPB=90゜;
此时∠OQP=∠BQP、∠QBP=∠ABP,由(1)题图可知:OP=AP=PD;
∴OP=AP=
 OA=4
OA=4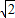 ,即 P(4
,即 P(4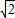 ,0);
,0);设抛物线的解析式为:y=a(x-4
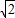 )2,代入点B(8
)2,代入点B(8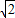 ,8),得:
,8),得:a(8
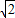 -4
-4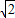 )2=8,解得 a=
)2=8,解得 a=
∴抛物线的解析式为:y=
 (x-4
(x-4 )2=
)2= x2-2
x2-2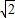 x+8.
x+8.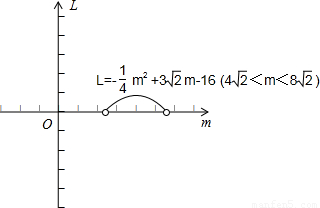 ②设直线BP的解析式为:y=kx+b,代入B(8
②设直线BP的解析式为:y=kx+b,代入B(8 ,8)、P(4
,8)、P(4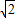 ,0),得:
,0),得: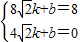 ,解得
,解得 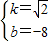
∴直线BP:y=
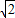 x-8.
x-8.已知点M的横坐标为m,则 M(m,
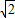 m-8)、N(m,
m-8)、N(m, m2-2
m2-2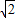 m+8),则有:
m+8),则有:MN的长:L=
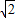 m-8-(
m-8-( m2-2
m2-2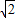 m+8)=-
m+8)=- m2+3
m2+3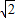 m-16(4
m-16(4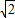 <m<8
<m<8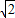 )(如右图)
)(如右图)配方,得:L=-
 (m2-12
(m2-12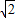 m+72)+2=-
m+72)+2=- (m-6
(m-6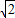 )2+2,
)2+2,∴当m取6
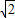 时,L有最大值,且最大值为 2.
时,L有最大值,且最大值为 2.点评:此题主要考查的是相似三角形以及二次函数的相关知识,题目的难度逐题递进,前面的题目为后面的解答过程提供了很好的铺垫,这样也降低了解题的难度.在解题时,一定要注意合理利用图形的辅助作用.另外,在求函数解析式和画函数图象时,要注意自变量的取值范围.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,已知:正△OAB的面积为
如图,已知:正△OAB的面积为 长线交于点E.
长线交于点E.


 ,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;
,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;