��Ŀ����
����Ŀ����ͼ������������y=ax�뷴��������y= ![]() ��x��0����ͼ���ڵ�M��
��x��0����ͼ���ڵ�M�� ![]() ��
�� ![]() ����
����
��1���������������ı���ʽ��
��2����ͼ1������AMB=90�㣬�������߷ֱ�����������������ύ�ڵ�A��B�����ı���OAMB�������
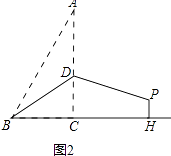
��3����ͼ2����P�Ƿ���������y= ![]() ��x��0����ͼ����һ�㣬����P��x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F��PF��ֱ��OM�ڵ�H������x��Ĵ��ߣ�����ΪG�����P�ĺ�����Ϊm����m��
��x��0����ͼ����һ�㣬����P��x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F��PF��ֱ��OM�ڵ�H������x��Ĵ��ߣ�����ΪG�����P�ĺ�����Ϊm����m�� ![]() ʱ���Ƿ���ڵ�P��ʹ���ı���PEGHΪ�����Σ������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
ʱ���Ƿ���ڵ�P��ʹ���ı���PEGHΪ�����Σ������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����M�� ![]() ��
�� ![]() ���ֱ����y=ax��y=
���ֱ����y=ax��y= ![]() �ã�
�ã�
![]() =a
=a ![]() ��
�� ![]() =
= ![]() ��
��
��ã�a=1��k=6��
�������������ı���ʽ�ֱ�Ϊ��y=x��y= ![]()
��2��
�⣺��ͼ1�У�����M�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪC��D��
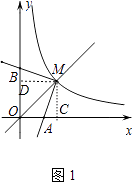
���MCA=��MDB=90�㣬��AMC=��BMD=90�㩁��AMD��MC=MD= ![]() ��
��
���AMC�ա�BMD��
��S�ı���OCMD=S�ı���OAMB=6
��3��
�⣺��P������Ϊ��x�� ![]() ������PE=HG=GE=
������PE=HG=GE= ![]() ��OE=x��
��OE=x��
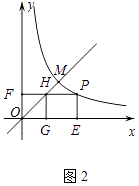
�ߡ�MOE=45�㣬
��OG=GH= ![]() ��
��
��OE=OG+GH= ![]() ��
��
��x= ![]() ��
��
���x=2 ![]() ��
��
��P��������2 ![]() ��
�� ![]() ��
��
����������1�����ô���ϵ�������ɽ�����⣮��2������֤����AMC�ա�BMD���Ƴ�S�ı���OCMD=S�ı���OAMB �� ���ɽ�����⣮��3����P������Ϊ��x�� ![]() ������PE=HG=GE=
������PE=HG=GE= ![]() ��OE=x��
��OE=x��

 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д�