题目内容
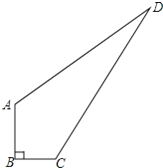
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F,AD=4,AB=6.
(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求![]() 的值.
的值.
【答案】(1)见解析;(2)AC=2![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
试题分析:(1)根据两个角对应相等的两个三角形相似证明即可;
(2)根据相似三角形的对应边的比相等列出比例式,计算即可;
(3)根据直角三角形斜边上的中线是斜边的一半得到CE=AE,证明△AFD∽△CFE,根据相似三角形的性质解答即可.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB;
(2)解:∵△ADC∽△ACB,
∴![]() =
=![]() ,即AC2=ADAB=24,
,即AC2=ADAB=24,
解得,AC=2![]() ;
;
(3)解:∵E为AB的中点,
∴CE=![]() AB=AE,
AB=AE,
∴∠EAC=∠ECA;
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
∴△AFD∽△CFE,
∴![]() =
=![]() ,
,
∵CE=![]() AB=3,AD=4,
AB=3,AD=4,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.

练习册系列答案
相关题目