题目内容
【题目】如图，在△ABC中，AB=24，AC=18，D是AC上一点，AD=6，在AB上取一点E，使A、D、E三点组成的三角形与△ABC相似，则AE的长为( )
A.8B.
C.8或D.8或9
【答案】C
【解析】
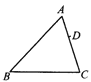
要考虑到在AB上取一点E，使A，D，E三点组成的三角形与△ABC相似情况有两种，一是过D作DE∥BC，二是在AB上取一点E，使△ADE～△ABC.
如图，情况分两种：解：
要在AB上取一点E，使A，D，E三点组成的三角形与△ABC相似情况有两种，
(1)过D作DE∥BC，交AB于点E
在△ABC中，∵EF∥AB
∴△ADE～△ACB， 
∵AB＝24，AC＝18， AD＝6
∴ 
= 
∵AE＝8
(2)在AB上取 一点E，使△ADE～△ABC
，即
= 
∴AE=
故答案为：c
练习册系列答案
阳光课堂课时作业系列答案
相关题目
