题目内容
【题目】某高科技公司根据市场需求,计划生产A,B两种型号的医疗器械.其部分信息如下:
信息一:每台A型器械的售价为24万元,每台B型器械的售价为30万元,每台B型器械的生产成本比A型器械的生产成本多5万元.
信息二:若销售3台A型器械和5台B型器械,共获利37万元;
根据上述信息,解答下列问题:
(1)求每台A型器械、每台B型器械的生产成本各是多少万元?
(2)若A,B两种型号的医疗器械共生产80台,且该公司所筹生产医疗器械资金不少于1800万元,但不超过1810万元,且把所筹资金全部用于生产此两种医疗器械,根据市场调查,每台A型医疗器械的售价将会提高a万元(a>0),每台B型医疗器械的售价不会改变,该公司应该如何生产可以获得最大利润?
【答案】(1)每台A型器械的生产成本是20万元,则每台B型器械的生产成本是25万元;(2)当a>1时,生产A种器械40台,B种器械40台,获得最大利润,当a=1时,三种方案利润都为400万元;当0<a<1时,生产A种器械38台,B种器械42台,获得最大利润.
【解析】
(1)设每台A型器械的生产成本是y万元,则每台B型器械的生产成本是(y+5)万元,(2)根据“销售3台A型器械和5台B型器械,共获利37万元”。列出方程,即可求解;
(3)设该公司生产A种疗器械x台,则生产B种医疗器械(80-x)台,列出不等式组,求出x的范围,再取整数,根据条件,得到利润关于x的函数,对参数a分类讨论,即可得到结论.
(1)设每台A型器械的生产成本是y万元,则每台B型器械的生产成本是(y+5)万元,
依题意得:3(24-y)+5[30-(y+5)]=37,
解得:y=20,
y+5=20+5=25,
答:每台A型器械的生产成本是20万元,则每台B型器械的生产成本是25万元;
(2)设该公司生产A种疗器械x台,则生产B种医疗器械(80-x)台,
依题意得: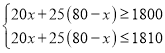 ,
,
解得38≤x≤40,
取整数得:x=38,39,40,
∴该公司有3种生产方案:
方案一:生产A种器械38台,B种器械42台.
方案二:生产A种器械39台,B种器械41台.
方案三:生产A种器械40台,B种器械40台.
依题意得,W=(24-20+a)x+(30-25)(80-x)=(4+a)x+400-5x=(a-1)x+400,
当a-1>0,即a>1时,生产A种器械40台,B种器械40台,获得最大利润,
当a-1=0,即a=1时,三种方案利润都为400万元;
当a-1<0,即0<a<1时,生产A种器械38台,B种器械42台,获得最大利润.

 阅读快车系列答案
阅读快车系列答案