题目内容
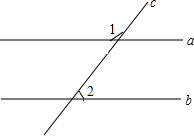
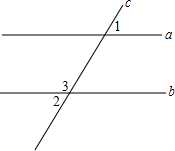 如图,直线a、b被c所截,若∠1=50°,∠2=________度时,a∥b;若a∥b,且∠1=50°时,∠3=________度.
如图,直线a、b被c所截,若∠1=50°,∠2=________度时,a∥b;若a∥b,且∠1=50°时,∠3=________度.
50 130
分析:本题首先应根据同位角相等判定两直线平行,再根据平行线的性质及邻补角的性质求出∠3的度数.
解答: 解:∵∠4=∠2(对顶角相等),
解:∵∠4=∠2(对顶角相等),
又∵∠4=∠1时,a∥b(同位角相等,两直线平行);
∴∠2=∠1;
∵∠1=50°,
∴∠2=50°;
∵a∥b,
∴∠4=∠1(两直线平行,同位角相等);
又∵∠3=180°-∠4,∠1=50°,
∴∠3=180°-50°=130°.
故答案为:50、130.
点评:本题主要考查的是平行线的判定与性质.本题主要利用了“内错角相等,两直线平行”的判定定理及“两直线平行,同位角相等”的性质.
分析:本题首先应根据同位角相等判定两直线平行,再根据平行线的性质及邻补角的性质求出∠3的度数.
解答:
 解:∵∠4=∠2(对顶角相等),
解:∵∠4=∠2(对顶角相等),又∵∠4=∠1时,a∥b(同位角相等,两直线平行);
∴∠2=∠1;
∵∠1=50°,
∴∠2=50°;
∵a∥b,
∴∠4=∠1(两直线平行,同位角相等);
又∵∠3=180°-∠4,∠1=50°,
∴∠3=180°-50°=130°.
故答案为:50、130.
点评:本题主要考查的是平行线的判定与性质.本题主要利用了“内错角相等,两直线平行”的判定定理及“两直线平行,同位角相等”的性质.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 23、完成下列推理过程:
23、完成下列推理过程: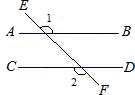 14、如图,直线AB,CD被EF所截,且AB∥CD,如果∠1=135°,那么∠2=
14、如图,直线AB,CD被EF所截,且AB∥CD,如果∠1=135°,那么∠2=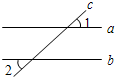 12、如图,直线a,b被直线c所截,若a∥b,∠1=45°,则∠2=
12、如图,直线a,b被直线c所截,若a∥b,∠1=45°,则∠2=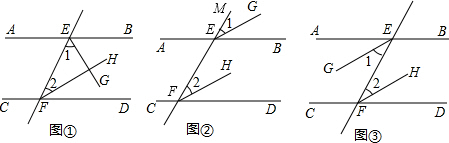
 如图,直线a、b被直线c所截,若a∥b,∠1=125°,则∠2等于( )
如图,直线a、b被直线c所截,若a∥b,∠1=125°,则∠2等于( )