题目内容
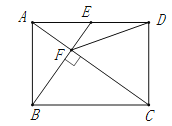
【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④tan∠CAD＝．其中正确的结论有( )
A.4个 B．3个 C．2个 D．1个
【答案】B.
【解析】
试题分析：∵矩形ABCD中，∴AD∥BC.∴△AEF∽△CAB，所以①正确；∵△AEF∽△CAB，∴＝＝，∴CF＝2AF，所以②正确；过点D作DH⊥AC于点H.易证△ABF≌△CDH(AAS).∴AF＝CH.∵EF∥DH,∴＝ ＝1.∴AF＝FH.∴FH＝CH.∴DH垂直平分CF.∴DF＝DC.所以③正确；设EF＝1，则BF＝2.∵△ABF∽△EAF.∴＝.∴AF＝＝＝.∴tan∠ABF＝＝.∵∠CAD＝∠ABF，∴tan∠CAD＝tan∠ABF＝.，所以④错误.故答案选B.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
