题目内容
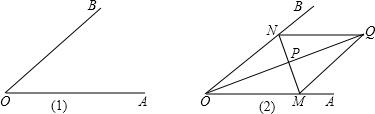
23、如果给你一副带有刻度的三角板,请你画出∠AOB的平分线.下面三位同学是这样设计的,
(1) 小亮是这样做的:
①分别在OA,OB上量取OM=ON,连接MN.
②取MN的中点P.
③作射线OP
那么OP是∠AOB的平分线

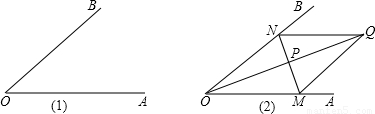
(2)小明是这样做的:
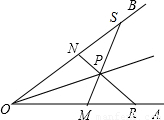
①分别在OA,OB上量取OM=ON,MR=NS
②连接MS,NR交于P
③作射线OP
那么OP是∠AOB的平分线.那么OP是∠AOB的平分线.
(1)以上2位同学的设计你认为正确吗?若正确,请对正确做法加以证明,若不正确,请简要说明理由.
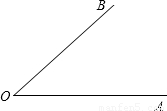
(2)请你根据以上信息,创造新的证明角平分线的做法,在备用图上画出图形,并证明其可行性.
(1) 小亮是这样做的:
①分别在OA,OB上量取OM=ON,连接MN.
②取MN的中点P.
③作射线OP
那么OP是∠AOB的平分线

(2)小明是这样做的:
①分别在OA,OB上量取OM=ON,MR=NS
②连接MS,NR交于P
③作射线OP
那么OP是∠AOB的平分线.那么OP是∠AOB的平分线.

(1)以上2位同学的设计你认为正确吗?若正确,请对正确做法加以证明,若不正确,请简要说明理由.
(2)请你根据以上信息,创造新的证明角平分线的做法,在备用图上画出图形,并证明其可行性.

分析:(1)小亮根据全等三角形的判定定理SSS即可证出答案;小明根据全等三角形的判定SAS得到△ONR≌△OMS,推出∠OSM=∠ORN,即可证出△NSP≌△MPR和△ONP≌△OMP,能推出∠MOP=∠POA,即可得到答案.
(2)由作法可知MO=MP和MP∥OA,可推出∠MOP=∠MPO=∠POA,即可得到答案.
(2)由作法可知MO=MP和MP∥OA,可推出∠MOP=∠MPO=∠POA,即可得到答案.
解答: 解:(1)都正确.
解:(1)都正确.
小亮的证明过程;
∵ON=OM,NP=PM,OP=OP
∴△ONP≌△OMP(SSS)
∴∠NOP=∠MOP,
即:OP是∠AOB的平分线.
小明的证明过程:
∵ON=OM,NS=SM
∴OS=OR
∵∠MON=∠MON
∴△ONR≌△OMS(SAS)
∠OSM=∠ORN
∴△NSP≌△MPR(AAS)
∴NP=MP
∴△ONP≌△OMP(SSS)
∴∠NOP=∠MOP,
即:OP是∠AOB的平分线.
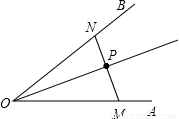
(2)解:可以这样做:
①在OB上任取一点M
②过M作MN∥OA,在MN上量取MP=OM
③作射线OP
则OP是∠AOB的平分线.
证明:
∵MO=MP,
∴∠MON=∠MPN,
∵MP∥OA
∴∠MPO=∠POA,
∴∠MOP=∠POA,
即OP是∠AOB的平分线.
 解:(1)都正确.
解:(1)都正确.小亮的证明过程;
∵ON=OM,NP=PM,OP=OP
∴△ONP≌△OMP(SSS)
∴∠NOP=∠MOP,
即:OP是∠AOB的平分线.
小明的证明过程:
∵ON=OM,NS=SM
∴OS=OR
∵∠MON=∠MON
∴△ONR≌△OMS(SAS)
∠OSM=∠ORN
∴△NSP≌△MPR(AAS)
∴NP=MP
∴△ONP≌△OMP(SSS)
∴∠NOP=∠MOP,
即:OP是∠AOB的平分线.
(2)解:可以这样做:
①在OB上任取一点M
②过M作MN∥OA,在MN上量取MP=OM
③作射线OP
则OP是∠AOB的平分线.
证明:
∵MO=MP,
∴∠MON=∠MPN,
∵MP∥OA
∴∠MPO=∠POA,
∴∠MOP=∠POA,
即OP是∠AOB的平分线.
点评:本题主要考查了全等三角形的性质和判定,作图与基本作图,平行线的性质,三角形的角平分线等知识点,解此题的关键是能灵活运用性质进行证明和作图.

练习册系列答案
相关题目