题目内容
已知m,n分别是方程x2-x-2=0的两个实数根,那么对于一次函数y=mx+n,有以下六个判断:
①图象一定经过第一、三、四象限;②图象一定经过第一、二、四象限;
③图象一定经过第一、四象限; ④图象一定经过点(0,-1);
⑤y一定随x的增大而增大;⑥图象与两个坐标轴所围成的图形面积一定是2.
其中正确的判断是
- A.①④⑤
- B.②⑥
- C.③④⑤⑥
- D.③
D
分析:首先解方程求得m,n的值,即可确定一次函数的解析式,然后根据一次函数的性质即可作出判断.
解答:解方程x2-x-2=0得:x=2或-1.则m=2,n=-1或m=-1,n=2.
则函数y=mx+n就是y=2x-1或y=-x+2.
函数y=2x-1经过第一,三,四象限,y=-x+2经过第一,二,四象限.
故①②错误;③正确.
y=-x+2中令x=0,则y=2,故一定不经过(0,-1),故④错误;
y=-x+2中y随x的增大而减小,故⑤错误;
y=2x-1与x轴的交点坐标是:( ,0),与y轴的交点坐标是:(0,-1),则图象与两个坐标轴所围成的图形面积一定是
,0),与y轴的交点坐标是:(0,-1),则图象与两个坐标轴所围成的图形面积一定是 ×
× ×1=
×1= ,故⑤错误.
,故⑤错误.
故正确的是③.
故选D.
点评:本题主要考查了一元二次方程的解法,以及一次函数的性质,正确掌握一次函数的性质是关键.
分析:首先解方程求得m,n的值,即可确定一次函数的解析式,然后根据一次函数的性质即可作出判断.
解答:解方程x2-x-2=0得:x=2或-1.则m=2,n=-1或m=-1,n=2.
则函数y=mx+n就是y=2x-1或y=-x+2.
函数y=2x-1经过第一,三,四象限,y=-x+2经过第一,二,四象限.
故①②错误;③正确.
y=-x+2中令x=0,则y=2,故一定不经过(0,-1),故④错误;
y=-x+2中y随x的增大而减小,故⑤错误;
y=2x-1与x轴的交点坐标是:(
 ,0),与y轴的交点坐标是:(0,-1),则图象与两个坐标轴所围成的图形面积一定是
,0),与y轴的交点坐标是:(0,-1),则图象与两个坐标轴所围成的图形面积一定是 ×
× ×1=
×1= ,故⑤错误.
,故⑤错误.故正确的是③.
故选D.
点评:本题主要考查了一元二次方程的解法,以及一次函数的性质,正确掌握一次函数的性质是关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
已知两圆半径分别是方程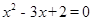 的两根,两圆圆心距为3,则两圆位置关系是( )
的两根,两圆圆心距为3,则两圆位置关系是( )
| A.外切 | B.外离 | C.相交 | D.内切 |
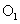 与⊙
与⊙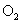 的半径
的半径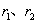 分别是方程
分别是方程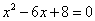 的两实根,若⊙
的两实根,若⊙