题目内容
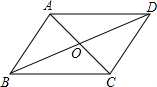 如图,长度不等的两根牙签AC、BD的中点O重合,问顺次连接各端点A、B、C、D所得四边形是什么特殊四边形?为什么?请补充完成下面的解答过程.
如图,长度不等的两根牙签AC、BD的中点O重合,问顺次连接各端点A、B、C、D所得四边形是什么特殊四边形?为什么?请补充完成下面的解答过程.解:所得四边形ABCD为
平行四边形
平行四边形
理由如下:因为O为AC、BD的中点
所以OA=
OC
OC
,OB=OD
OD
所以四边形ABCD为
平行四边形
平行四边形
根据是
对角线互相平分的四边形是平行四边形
对角线互相平分的四边形是平行四边形
.分析:根据平行四边形的判定定理(对角线互相平分的四边形是平行四边形)推出即可.
解答:解:四边形ABCD是平行四边形,
理由是:∵O为AC何BD的中点,
∴AO=OC,OB=OD,
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),
故答案为:平行四边形,OC,OD,平行四边形,对角线互相平分的四边形是平行四边形.
理由是:∵O为AC何BD的中点,
∴AO=OC,OB=OD,
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),
故答案为:平行四边形,OC,OD,平行四边形,对角线互相平分的四边形是平行四边形.
点评:本题考查了平行四边形的判定定理的应用,注意:对角线互相平分的四边形是平行四边形.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
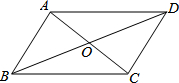 如图,我们使长度不等的两根牙签AC、BD的中点O重合,那么顺次连接各端A、B、C、D所得四边形是什么特殊四边形?你如何判断的?(请补充完成下面的解答过程)
如图,我们使长度不等的两根牙签AC、BD的中点O重合,那么顺次连接各端A、B、C、D所得四边形是什么特殊四边形?你如何判断的?(请补充完成下面的解答过程)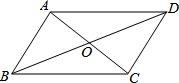 如图,我们使长度不等的两根牙签AC、BD的中点O重合,那么顺次连接各端A、B、C、D所得四边形是什么特殊四边形?你如何判断的?(请补充完成下面的解答过程)
如图,我们使长度不等的两根牙签AC、BD的中点O重合,那么顺次连接各端A、B、C、D所得四边形是什么特殊四边形?你如何判断的?(请补充完成下面的解答过程)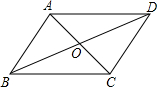 如图,长度不等的两根牙签AC、BD的中点O重合,问顺次连接各端点A、B、C、D所得四边形是什么特殊四边形?为什么?请补充完成下面的解答过程.
如图,长度不等的两根牙签AC、BD的中点O重合,问顺次连接各端点A、B、C、D所得四边形是什么特殊四边形?为什么?请补充完成下面的解答过程.