Question

【题目】如图，在平面直角坐标系xOy中，过点A(-6,0)的直线 与直线 ：y＝2x相交于点B(m，4)，

（1）求直线 的表达式；
（2）过动点P(n,0)且垂直于x轴的直线与 ， 的交点分别为C，D，当点C位于点D上方时，求出n的取值范围．

Answer 1

【答案】
（1）解：∵点B在直线l2上 ，∴4=2m，∴m=2，设l1的表达式为y=kx+b，
由A、B两点均在直线l1上得到， ，
解得： ，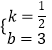
则l1的表达式为
（2）解：由图可知：C（ ，n），D（2n，n），
点C在点D的上方，所以， ，
解得：n＜2
【解析】（1）先根据正比例函数解析式求出点B的坐标，再根据点A、B的坐标，利用待定系数法求出直线AB的函数解析式即可。
（2）根据过动点P(n,0)且垂直于x轴的直线与 l1 ， l2 的交点分别为C，D，可表示出点C、D的坐标，再根据点C位于点D上方，列出关于n的不等式，求解即可。
【考点精析】根据题目的已知条件，利用确定一次函数的表达式的相关知识可以得到问题的答案，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．