题目内容
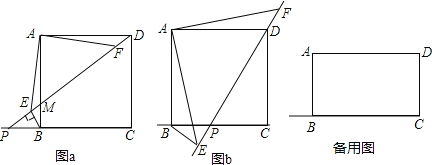
【题目】如图,正方形ABCD,点P在射线CB上运动(不包含点B、C),连接DP,交AB于点M,作BE⊥DP于点E,连接AE,作∠FAD=∠EAB,FA交DP于点F.
(1)如图a,当点P在CB的延长线上时,
①求证:DF=BE;
②请判断DE、BE、AE之间的数量关系并证明;
(2)如图b,当点P在线段BC上时,DE、BE、AE之间有怎样的数量关系?请直接写出答案,不必证明;
(3)如果将已知中的正方形ABCD换成矩形ABCD,且AD:AB=![]() :1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
:1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
【答案】(1)详见解析;②DE=BE+![]() AE,理由详见解析;(2)DE=
AE,理由详见解析;(2)DE=![]() AE﹣BE;(3)DE=2AE+
AE﹣BE;(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
【解析】
(1)①由正方形的性质得到AD=AB,∠BAD=90°,判断出△ABE≌△ADF,即可;②由①得到△ABE≌△ADF,并且判断出△EAF为直角三角形,用勾股定理即可;
(2)先由正方形的性质和已知条件判断出△ABE≌△ADF,再用判断出△EAF为直角三角形,用勾股定理即可;
(3)分两种情况讨论,先由正方形的性质和已知条件判断出△ABE∽△ADF,AF=![]() AE,DF=
AE,DF=![]() BE,再判断出△EAF为直角三角形,用勾股定理结合图形可得结论.
BE,再判断出△EAF为直角三角形,用勾股定理结合图形可得结论.
证明:(1)①正方形ABCD中,AD=AB,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
在△ABE和△ADF中,
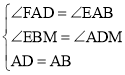 ,
,
∴△ABE≌△ADF,
∴DF=BE;
②DE=BE+![]() AE,
AE,
理由:由(1)有△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠BAE+∠FAM=∠DAF+∠FAM,
∴∠EAF=∠BAD=90°,
∴EF=![]() AE,
AE,
∵DE=DF+EF,
∴DE=BE+![]() AE;
AE;
(2)DE=![]() AE﹣BE;
AE﹣BE;
理由:正方形ABCD中,AD=AB,∠BAD=∠BAE+∠DAE=90°,
∵∠FAD=∠EAB,
∴∠EAF=∠BAD=90°,
∴∠AFE+∠AEF=90°
∵BE⊥DP,
∴∠BEA+∠AEF=90°,
∴∠BEA=∠AFE,
∵∠FAD=∠EAB,AD=AB
∴△ABE≌△ADF,
∴AE=AF,BE=DF
∵∠EAF=90°
∴EF=![]() AE,
AE,
∵EF=DF+DE=![]() AE,
AE,
∴DE=![]() AE﹣DF=
AE﹣DF=![]() AE﹣BE;
AE﹣BE;
(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
①如图1所示时,
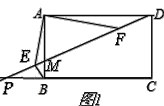
正方形ABCD中,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
∵∠FAD=∠EAB
∴△ABE∽△ADF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE
BE
∵∠FAD=∠EAB
∴∠EAF=∠EAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,
∴EF=![]() =2AE=DE﹣DF=DE﹣
=2AE=DE﹣DF=DE﹣![]() BE,
BE,
即:DE=2AE+![]() BE;
BE;
②如图2所示,
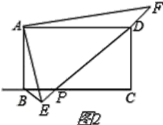
∵∠DAF=∠BAE,
∴∠EAF=∠BAD=90°,
∵∠DAF=∠BAE,
∴△BAE∽△DAF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE,
BE,
∵∠EAF=90°,
根据勾股定理得,EF=![]() =2AE=DE+DF=DE+
=2AE=DE+DF=DE+![]() BE,
BE,
∴DE=2AE﹣![]() BE.
BE.

【题目】我国农村劳动力人数有4.8亿.从目前来看,我国农民的科技水平还不高,在农村4.8亿的劳动力中,小学文化程度以下的占40%,具有初中文化程度的占48%,具有高中文化程度的占12%,受过职业技术培训的占5%,但据专家统计,他们中八成以上会进行分数、平均数、增长率等基本数学运算,能基本适应当代经济生活,这是初等数学教育的一大成就.
请根据上面的数据信息解答下列问题:
文化程度 | 人数(亿) | 会基本数学运算人数(亿) | 百分比 |
小学以下 | 1.4976 | ||
初中文化 | 2.0736 | 90% | |
高中文化 | 95% | ||
受过职业技术培训 | 0.2328 | 97% |
(1)填写下列农民受教育情况及掌握基本数学运算情况统计
(2)根据图表,求出农村劳动力中会进行基本数学运算的总人数占农村劳动力总人数的百分比;
(3)政府计划两年后使农村劳动力初、高中文化程度达到80%,那么平均每年增长的百分率是多少(精确到0.1%)?