题目内容
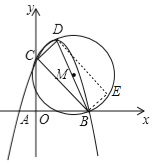
【题目】如图,二次函数![]() (a<0)的图象与x轴交于A,B两点(点B在点A的右侧),与y轴的正半轴交于点C,顶点为D.若以BD为直径的⊙M经过点C.
(a<0)的图象与x轴交于A,B两点(点B在点A的右侧),与y轴的正半轴交于点C,顶点为D.若以BD为直径的⊙M经过点C.

(1)请直接写出C,D的坐标(用含a的代数式表示);
(2)求抛物线的函数表达式;
(3)⊙M上是否存在点E,使得∠EDB=∠CBD?若存在,请求出所满足的条件的E的坐标;若不存在,请说明理由.
【答案】(1)C的坐标为(0,﹣3a),D的坐标为(1,﹣4a);(2)![]() ;(3)(4,1)、(
;(3)(4,1)、(![]() ,
,![]() ).
).
【解析】
试题分析:(1)计算横坐标为0的函数值即可得到C点坐标,然后将解析式配成顶点式即可得出点D的坐标;
(2)先利用二次函数与x轴的交点问题确定A点和B点坐标,再根据圆周角定理得到∠BCD=90°,则根据两点间的距离公式表示出BC,CD,BD,接着利用勾股定理建立方程,然后解方程求出a即可得到二次函数解析式;
(3)先计算出![]() ,
,![]() ,再根据圆周角定理,由∠EDB=∠CBD得弧CD=弧BE,则CD=BE,接着证明Rt△BED≌Rt△DCB,得到DE=BC,设E(x,y),根据两点间的距离公式得
,再根据圆周角定理,由∠EDB=∠CBD得弧CD=弧BE,则CD=BE,接着证明Rt△BED≌Rt△DCB,得到DE=BC,设E(x,y),根据两点间的距离公式得![]() ,
,![]() ,然后解方程组得x=4,y=1或x=
,然后解方程组得x=4,y=1或x=![]() ,y=
,y=![]() ,从而可得满足条件的E点坐标.
,从而可得满足条件的E点坐标.
试题解析:(1)当x=0时,![]() =﹣3a,则点C的坐标为(0,﹣3a);
=﹣3a,则点C的坐标为(0,﹣3a);
∵![]() =
=![]() ,∴点D的坐标为(1,﹣4a);
,∴点D的坐标为(1,﹣4a);
(2)当y=0时,![]() ,解得
,解得![]() ,
,![]() ,则A(﹣1,0),B(3,0),∵BD为⊙M的直径,∴∠BCD=90°,而
,则A(﹣1,0),B(3,0),∵BD为⊙M的直径,∴∠BCD=90°,而![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,在Rt△BCD中,∵
,在Rt△BCD中,∵![]() ,∴
,∴![]() ,整理得
,整理得![]() ,解得a=﹣1或a=1(舍去);∴抛物线解析式为:
,解得a=﹣1或a=1(舍去);∴抛物线解析式为:![]() ;
;
(3)存在.a=1,![]() ,
,![]() ,∵∠EDB=∠CBD,∴CD=BE,而BD为直径,∴∠BED=90°,∴Rt△BED≌Rt△DCB,∴DE=BC,设E(x,y),∴
,∵∠EDB=∠CBD,∴CD=BE,而BD为直径,∴∠BED=90°,∴Rt△BED≌Rt△DCB,∴DE=BC,设E(x,y),∴![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴![]() ,
,![]() ,解得x=4,y=1或x=
,解得x=4,y=1或x=![]() ,y=
,y=![]() ,∴满足条件的E点坐标为(4,1)、(
,∴满足条件的E点坐标为(4,1)、(![]() ,
,![]() ).
).