题目内容
（2002•荆门）如图，在⊙O中，P是直径AB上一动点，在AB同侧作AA′⊥AB，BB′⊥AB，且AA′=AP，BB′=BP，连接A′B′．当点P从点A移到点B时，A′B′的中点的位置（ ）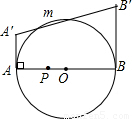
A．在平分AB的某直线上移动
B．在垂直AB的某直线上移动
C．在
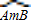上移动D．保持固定不移动
【答案】分析：此题根据梯形的中位线定理，首先明确A′B′的中点的位置在过点O垂直于AB的直线上，再根据梯形的中位线定理，得到要求的中点到点O的距离是一个定值，即可说明该中点是一个定点．
解答：解：由题意知，四边形AA′B′B是直角梯形．
设A′B′的中点为D，则OD是直角梯形的中位线，即OD⊥AB．
又OD=
（AA′+BB′）=
（AP+BP）=
AB．
故OD的长又是定值，则点D是一定点．
故选D．
点评：本题要熟练运用梯形的中位线定理进行分析．
解答：解：由题意知，四边形AA′B′B是直角梯形．
设A′B′的中点为D，则OD是直角梯形的中位线，即OD⊥AB．
又OD=
（AA′+BB′）=（AP+BP）=AB．故OD的长又是定值，则点D是一定点．
故选D．
点评：本题要熟练运用梯形的中位线定理进行分析．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
（2002•荆门）如图，两平面镜α、β的夹角为θ，入射光线AO平行于β入射到口上，经两次反射后的出射光线O'B平行于α，则角θ等于
+b
