Question

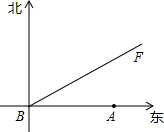（2011•岳池县模拟）如图，某气象站测得台风中心在A城正西方向300km的B处，以每小时10

7

km的速度向北偏东60°的BF方向移动，距台风中心200km的范围是受台风干扰的区域，问A城是否受到此次台风的干扰？为什么？若要受到台风干扰，求出A城受台风干扰的时间．

Answer 1

分析：作AM⊥BF，则得出∠AMB．根据∠FBA=30°，可得出AM的长，则A城会受到此次台风的干扰；以A为圆心，200km为半径作弧交BF于C₁、C₂两点，连接AC₁=AC₂，在Rt△AMC₁中有C₁M的长，可得出C₁C₂，从而得出A城受台风干扰的时间．

解答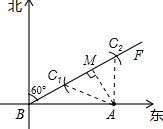：解：作AM⊥BF于点M，则∠AMB=90°．
∵∠FBA=90°-60°=30°，
∴AM=

1

2

AB=

1

2

•300=150＜200，
∴A城会受到此次台风的干扰，以A为圆心，200km为半径作弧交BF于C₁、C₂两点，连接AC₁=AC₂．
∵AM⊥BF，
∴C₁C₂=2C₁M．
在Rt△AMC₁中，有C₁M=

2002-1502

=50

7

(km)，
∴C₁C₂=100

7

km，
∴A城受台风干扰的时间为：

100 7

10 7

=10（小时）．

点评：本题考查了含30度角的直角三角形以及勾股定理，是基础知识要熟练掌握．