Question

（2011•岳池县模拟）如图，在平面直角坐标系xoy中，双曲线y1=

k

x

与直线y₂=k′x+b交于点A、E两点．AE交x轴于点C，交y轴于点D，AB⊥x轴于点B，C为OB中点．若D点坐标为（0，-2）且S_△AOD=4．
（1）求双曲线与直线AE的解析式．
（2）求E点的坐标．
（3）观察图象，写出y₁＞y₂时x的取值范围．

Answer 1

分析：（1）需求A点坐标，由S_△AOD=4，点D（0，-2），可求A的横坐标；由C是OB的中点，可得OD=AB求出A点纵坐标，从而求出反比例函数解析式；根据A、D两点坐标求一次函数解析式；
（2）根据（1）中所求出双曲线解析式和直线AE的解析式组成方程组，求出x，的值，再根据E所在的象限即可求出它的坐标；
（3）观察图象知，分两种情况讨论，当y₁＞y_{2时得出x的取值范围}；

解答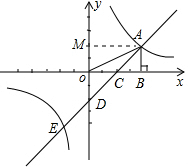：解：（1）作AM⊥y轴于点M，
∵D（0，-2），
∴DO=2，
∵S_△AOD=4且AM⊥y轴，
∴

1

2

•2AM=4，
∴AM=4．
∵y轴⊥x轴，AB⊥x轴，
∴∠ABC=∠DOC=90°．
∵C为OB中点，
∴BC=OC．
∵∠ACB=∠DCO，
∴△ABC≌△DOC（ASA），
∴AB=DO=2，
∴A（4，2）．
∵双曲线过A，
∴

k

4

=2
∴k=8，
∴双曲线解析式为：y=

8

x

．
∵直线AE过A（4，2）与D（0，-2），
∴

4k′+b=2 b=-2

，
解之得

k′=1 b=-2

，
∴直线AE解析式为：y=x-2；

（2）根据（1）得：

y= 8 x y=x-2

，
解得

x1=-2 y1=-4

x2=4 y2=2

，
根据E所在的象限得，E（-2，-4）；

（3）在y轴的右侧，当y₁＞y₂时，x的取值范围是：0＜x＜4，
在y轴的左侧，当y₁＞y₂时，x的取值范围是x＜-2，
所以y₁＞y₂时x的取值范围是：0＜x＜4或x＜-2．

点评：此题考查了反比例函数的综合；熟练掌握通过求点的坐标进一步求函数解析式的方法；通过观察图象解不等式时，从交点看起，函数图象在上方的函数值大．