题目内容
(1)如图,点D在△ABC的边BC上,连结AD,在线段AD上任取一点E,求证:∠BEC=∠ABE+∠ACE+∠BAC.
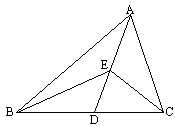
(2)已知点D在△ABC的边BC上,点E是线段AD所在直线上的任意一点,其中点E与点A、D不重合,且点E在△ABC的形外,连结BE、CE,请画满足上述条件的图形,并写出∠BEC、∠ABE、∠ACE、∠BAC之间的关系式.
答案:
解析:
解析:
|
(1) (2)有两种情况,如图答Ⅰ,此时,∠BAC=∠ABE+∠ACE+∠BEC;或如图答Ⅱ,此时,∠BEC+∠ABE+∠ACE+∠BAC=
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
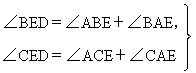
 26、点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
26、点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点. 如图,点C在线段AB上,点M、N分别是AC、BC的中点.若AC=9cm,CB=6cm,求线段MN的长.
如图,点C在线段AB上,点M、N分别是AC、BC的中点.若AC=9cm,CB=6cm,求线段MN的长.

 (2012•太原二模)如图,点A在反比例函数
(2012•太原二模)如图,点A在反比例函数