题目内容
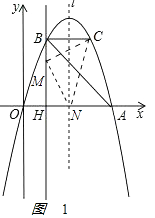
【题目】如图,抛物线y=ax2+bx经过A(4,0),B(1,3)两点,点B、C关于抛物线的对称轴l对称,过点B作直线BH⊥x轴,交x轴于点H.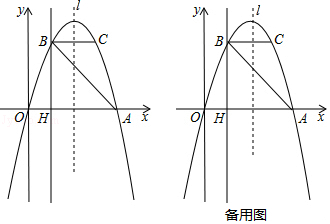
(1)求抛物线的解析式;
(2)若点M在直线BH上运动,点N在x轴上运动,是否存在这样的点M、N,使得以点M为直角顶点的△CNM是等腰直角三角形?若存在,请求出点M、N的坐标;若不存在,请说明理由.
【答案】
(1)
解:把点A(4,0),B(1,3)代入抛物线y=ax2+bx中,
得 ![]()
解得: ![]() ,
,
∴y=﹣x2+4x
(2)
解:∵抛物线y=﹣x2+4x的对称轴为x=2,
又点B的坐标为(1,3),点B、C关于抛物线的对称轴对称,
∴点C的坐标为(3,3).
假设存在这样的点M、N,使得以点M为直角顶点的△CNM是等腰直角三角形.
①当M在x轴上方时,如图1
 ,
,
∵∠CMB+∠HMN=90°,∠HMN+∠HNM=90°,
∴∠CMB=∠MNH.
在△CBM和△MHN中
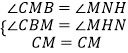 ,
,
△CBM≌△MHN(AAS),
∴BC=MH=2,BM=HN=3﹣2=1,
∴M(1,2),N(2,0).
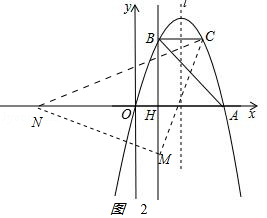
②M在x轴下方时,如图2
 ,
,
∵∠CMB+∠HMN=90°,∠HMN+∠HNM=90°,
∴∠CMB=∠MNH.
在△CBM和△MHN中
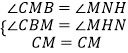 ,
,
△CBM≌△MHN(AAS),
∴HM=CB=2,HN=MB=2+3=5,
∴M(1,﹣2),N(﹣4,0).
综上所述,存在这样的点M(1,2),N(2,0)或M(1,﹣2),N(﹣4,0)使得以点M为直角顶点的△CNM是等腰直角三角形
【解析】(1)根据待定系数法,可得函数解析式;(2)根据全等三角形的判定与性质,可得MH,HN的值,根据点的坐标,可得答案.

练习册系列答案
相关题目