Question

【题目】某货运公司接到吨物资运载任务，现有甲、乙、丙三种车型的汽车供选择，每辆车的运载能力和运费如表：

车型	甲	乙	丙
汽车运载量(吨/辆)	5	8	10
汽车运费(元/辆)	400	500	600

（1）甲种车型的汽车辆，乙种车型的汽车辆，丙种车型的汽车辆，它们一次性能运载　　　　吨货物．

（2）若全部物资都用甲、乙两种车型的汽车来运送，需运费元，求需要甲、乙两种车型的汽车各多少辆？

（3）为了节省运费，该公司打算用甲、乙、丙三种车型的汽车共辆同时参与运送，请你帮货运公司设计派车方案；并求出各种派车方案的运费．

Answer 1

【答案】（1）74；（2）甲车型的汽车有8辆，乙车型的汽车有10辆；（3）派车方案有两种：甲车型的汽车有2辆，乙车型的汽车有10辆，丙车型的汽车有3辆，运费为7600元；甲车型的汽车有4辆，乙车型的汽车有5辆，丙车型的汽车有6辆，运费为7700元．

【解析】

（1）用每种车型的数量×各自的运载量，然后将结果相加即可得出答案；

（2）设甲车型的汽车有x辆，乙车型的汽车有y辆，根据题意列出二元一次方程组，解方程组即可得出答案；

（3）设甲车型的汽车有a辆，乙车型的汽车有b辆，丙车型的汽车有c辆，根据题意列出方程，再根据a,b,c都是正整数且a,b,c均不为0，即可确定a,b,c的值，进而可确定派车方案的运费．

（1）甲种车型的汽车辆，乙种车型的汽车辆，丙种车型的汽车辆，它们一次性能运载货物的数量为： （吨）；

（2）设甲车型的汽车有x辆，乙车型的汽车有y辆，根据题意有

解得

所以甲车型的汽车有8辆，乙车型的汽车有10辆；

（3）设甲车型的汽车有a辆，乙车型的汽车有b辆，丙车型的汽车有c辆，根据题意有

消去c得

∵a,b,c都是正整数，且a,b,c均不为0，

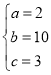∴ 或

∴派车方案有两种：甲车型的汽车有2辆，乙车型的汽车有10辆，丙车型的汽车有3辆；甲车型的汽车有4辆，乙车型的汽车有5辆，丙车型的汽车有6辆；

当时，运费为： （元）；

当时，运费为： （元）；

综上所述，派车方案有两种：甲车型的汽车有2辆，乙车型的汽车有10辆，丙车型的汽车有3辆，运费为7600元；甲车型的汽车有4辆，乙车型的汽车有5辆，丙车型的汽车有6辆，运费为7700元．