题目内容
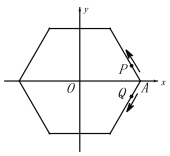
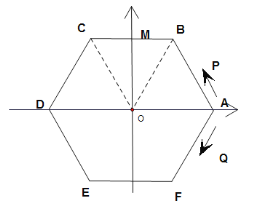
【题目】如图，点O为正六边形的中心，P，Q分别从点A（1，0）同时出发，沿正六边形按图示方向运动，点P的速度为每秒1个单位长度，点Q的速度为每秒2个单位长度，则第2020次相遇地点的坐标为（ ）
A.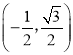
B.
C.
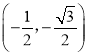D.
【答案】A
【解析】
根据题意可求出正六边形的周长，以及点P，Q相遇所需的时间为2秒，从而得出两点第一次相遇的地点为点C，第二次相遇的地点为点E，第三次相遇的地点为点A，第四次相遇的地点为点C，因此两点的相遇是3次一循环，
，因此第2020次相遇的地点为点C，求点C坐标即可．
解：由题意可得：
∴正六边形的周长为
∵点P的速度为每秒1个单位长度，点Q的速度为每秒2个单位长度
∴第一次相遇的时间为
此时点P的路程为
，点P，Q第一次相遇的地点为点C
依次类推，得出：
点P，Q第二次相遇的地点为点E，
点P，Q第三次相遇的地点为点A，
点P，Q第四次相遇的地点为点C，
∴点P，Q两点的相遇是3次一循环，
∵
∴第2020次相遇的地点为点C
∵
∴
∴
故选：A．
练习册系列答案
相关题目
